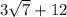(письменно) 1. История раненого коня.
2 Мельник Панкрат.
з филька по прозвищу «Ну тебя».
4 Рассказ бабки
5. Лютая зима.
босознание Филькой своего поступка.
7 Разговор Фильки с Панкратом.
8 Работа у мельницы.
9хлеб раненому коню.
10 Филька помирился с раненым конем.
Пусть диаметр большого круга МК, О – его центр, радиус=R, А и В - центры полукружий, их радиусы АО=ОВ=R/2. Центр вписанного третьего круга С, его радиус – r.
Соединим центры полукружий с центром вписанного в криволинейную фигуру круга. Как вписанный, он касается внутренним касанием окружности большего круга и внешним - полукружий. АС=ВС=(R/2 + r). Треугольник АВС - равнобедренный. AO=BO, ⇒ СО - его медиана и высота. По т.Пифагора АС²=АО²+СО² Для удобства записи примем R/2=a. Тогда АО=а, R=ОТ=2а, СО=(2а-r). Запишем (a+r)²=a²+(2a-r)². ⇒ a²+2ar+r²=a²+4a²-4ar+r². ⇒ 4а²-6ar=0. Сократив уравнение на 2а, получим 2а-3r=0, ⇒ 3r=2a=R. Радиус вписанного круга равен R/3. Все круги - подобны. Для данных k=1/3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. S(R/3):S(R)=k²=(1/3)²=1/9. ответ - в 9 раз площадь меньшего круга меньше площади большего круга.
1) Т.к. углы CDB и CAB опираются на одну и ту же дугу, то они равны. Тогда треугольники DCB и ABC равны по стороне и 2-м углам(AC общая, а углы CDB=DBC=CAB=BAC т.к. треугольники DCB и ABC равнобедренные и углы CDB=CAB см. выше). Треугольники DCA и ABD равны по тому же принципу. В итоге треугольники CTB и DTA равнобедренные, а т.к. углы CTB и DTA вертикальные, то углы TDA и TBC равны, а это признак параллельности прямых, тогда CB || AD.
2) Пусть ACB=α. По формуле радиуса описанной окружности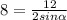 , тогда
, тогда  . Угол DCA=180-3α. По теореме синусов имеем
. Угол DCA=180-3α. По теореме синусов имеем 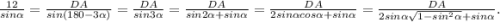 . Теперь подставляем значение sinα=3/4 и вычисляем. У меня получилось
. Теперь подставляем значение sinα=3/4 и вычисляем. У меня получилось