Пусть точки K, L, M лежат соответственно на сторонах AB, BC и AC правильного треугольника ABC, причём KL $ \perp$ BC, LM $ \perp$ AC, MK $ \perp$ AB. Тогда
Аналогично $ \angle$KML = 60o. Значит, треугольник KLM также равносторонний. Прямоугольные треугольники AKM, BLK и CML равны по гипотенузе и острому углу, а т.к. CM = AK = $ {\frac{{1}}{{2}}}$AM, то CM : AM = 1 : 2. Аналогично AK : KB = BL : LC = 1 : 2.
Так как наши графики являются прямыми, функции выглядят так:
Найдем значения k и b, подставив значения точек A и B в уравнение и решив следующую систему:
Найдем b, подставив в :
Первое уравнение имеет такой вид:
- - - - - -
Найдем второе уравнение по аналогии (мне лень расписывать системами, так что я буду писать просто через новую строчку и в конце запишу итоговое решение системы)
- - - - -
- - - - -
Второе уравнение имеет следующий вид:
Чтобы найти точку пересечения, нужно приравнять уравнения графиков.
Чтобы найти y, нужно подставить в любое уравнение значение x.
1 : 2
Объяснение:
Пусть точки K, L, M лежат соответственно на сторонах AB, BC и AC правильного треугольника ABC, причём KL $ \perp$ BC, LM $ \perp$ AC, MK $ \perp$ AB. Тогда
$\displaystyle \angle$MKL = 180o - $\displaystyle \angle$BKM - $\displaystyle \angle$LKB = 180o -90o -30o = 60o.
Аналогично $ \angle$KML = 60o. Значит, треугольник KLM также равносторонний. Прямоугольные треугольники AKM, BLK и CML равны по гипотенузе и острому углу, а т.к. CM = AK = $ {\frac{{1}}{{2}}}$AM, то CM : AM = 1 : 2. Аналогично AK : KB = BL : LC = 1 : 2.
(26;4)
Объяснение:
Так как наши графики являются прямыми, функции выглядят так: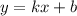
Найдем значения k и b, подставив значения точек A и B в уравнение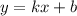
и решив следующую систему:
Найдем b, подставив в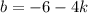
:
Первое уравнение имеет такой вид: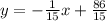
- - - - - -
Найдем второе уравнение по аналогии (мне лень расписывать системами, так что я буду писать просто через новую строчку и в конце запишу итоговое решение системы)
- - - - -
- - - - -
Второе уравнение имеет следующий вид: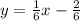
Чтобы найти точку пересечения, нужно приравнять уравнения графиков.
Чтобы найти y, нужно подставить в любое уравнение значение x.
ответ: (26;4)