Питання № 1 Що називають синусом кута α (0°≤α≤180°)? А ординату y точки M одиничного півкола, яка відповідає куту α. Б відношення абсциси x точки M одиничного півкола до ординати y, яка відповідає куту α. В абсцису x точки M одиничного півкола, яка відповідає куту α. Г відношення ординати y точки M одиничного півкола до абсциси x, яка відповідає куту α. Питання №2 ? Чому дорівнює cos⁡(90°-α)? А -sin ⁡α Б -cos⁡ α В sin ⁡α Г cos⁡ α Питання №3 ? 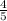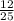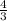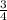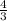Знайдіть tg α, якщо sin α = $\frac{3}{5}$ ;cos α = - $\frac{4}{5}$ A tg= α - $\frac{12}{25}$ Б tg α = - $\frac{4}{3}$ В tg α = - $\frac{3}{4}$ Г tg α = $\frac{4}{3}$ Питання №4 ? Знайдіть cos α, якщо sin α = 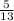$\frac{5}{13}$ , a tg α = - 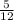$\frac{5}{12}$ А cos α =- 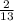$\frac{2}{13}$ Б cos α = 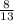$\frac{8}{13}$ В cos α = 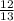$\frac{12}{13}$ Г cos α =- 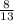$\frac{8}{13}$ Питання №5 ? Чому дорівнює значення виразу 4 cos 60° - 6 sin 30° А -1 Б 0 В 5 Г -5 Питання №6 ? Чому дорівнює cos(180°-α)? А sinα Б cosα В -cosα Г -sinα Питання №7 ? Як пов’язані між собою синус и косинус одного й того самого кута? А sin² α + cos²α = 1 Б (sin α + cos α)² = 1 В sin² α - cos² α =1 Г sin α + cos α = 1 Питання №9 ? Чому дорівнює значення виразу 4 cos120°-6 sin150° А 0 Б -5 В 5 Г -1

Показать ответ

Ответ:

ываывс

18.02.2020 20:18

Отрезки касательных, проведённые из одной точки, равны, значит, одна боковая сторона равна 2+32 = 34, вторая равна ей, меньшее основание равно 2+2 = 4, большее равно 32+32 = 64. Проводим две высоты к большему основанию, а также диаметр, перпендикулярный к основанию. Высоты и перпендикуляр параллельны, кроме того, отрезки высот отсекают на большем основании три отрезка, два из которых соответственно равны, а третий равен меньшему основанию, т.е. равен 4. Значит, равные отрезки, на которые делят высоты большее основание равны 1/2*(64-4) = 30. Далее по теореме Пифагора находим высоту, т.е. катет прямоугольного треугольника, который равен √(34²-30²) = √(1156-900) = √256 = 16.

0,0(0 оценок)

Ответ:

gyulmalievasab

01.10.2020 17:53

больше половины отрезка. получаем две точки их пересечения.
3. через эти точки проводим прямую до пересечения с первой окружностью. И соединяем эту точку с левой точкой нашей стороны. Это и будет поворот на 60 нашей стороны.
4.берем вторую сторону , измеряем ее длину из одной точки и измеряем расстояние от второго конца нашей первой стороны, которую мы уже повернули до дальнего края второй стороны.
5.от левого конца повернутой стороны строим две окружности измеренных радиусов и в точке их пересечения получаем второй конец второй стороны.
6. И т. д. с каждой стороной.
Нужно нарисовать пример поворота на 60 градусов против часовой стрелки семиугольника.