пл Найдите промежутки возрастания и убывания, точки максимума и точки минимума функции, ее максимумы и минимумы. Построить ее график.

1. =3−1

2. =−2+1

3. =2+1

4. =0.5−1.5

Показать ответ

Ответ:

yulia398

29.04.2020 12:32

1) радиус вписанной окружности равен 5

радиус описанной окружности равен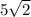 $5\sqrt{2}$

2) 4 - стороны у квадрата

Объяснение:

1) радиус вписанной окружности равен 5 см

2) это квадрат. Так как, если вписать в него окружность, то радиус этой окружности равен половине стороны квадрата.

То есть 10см (длина стороны квадрата) :2=5 см (длина радиуса вписанной окружности)

Ну у квадрата 4 стороны.

Если же это радиус описанной окружности, то он равен половине диагонали квадрата. По теореме Пифагора диагональ квадрата равна

$10^2+10^2=200=(10\sqrt{2})^2$

$10\sqrt{2}$ - диагональ данного квадрата

Теперь его половина равна

$10\sqrt{2} :2=5\sqrt{2}$

0,0(0 оценок)

Ответ:

diana0483

23.08.2022 22:00

два угла по 50° и два угла по 130°

Объяснение:

Пусть один из углов равен х - градусов, тогда вертикальный к нему равен тоже х градусов. Остальные два вертикальных угла равны (180-х)°. Так как односторонний к углу в х градусов равен (180-х)°, а таких угла два при пересечении двух прямых.

Сумма трех углов без первого угла в х градусов равна:

х+(180-х)+(180-х)=360-х (*)

По условию задачи известно, что эта сумма (*) больше градусной меры угла в х градусов на 260°.

Составим уравнение

360-х=х+260

360-260=х+х

100=2х

2х=100

х=100:2

х=50° - мера первого угла

180-50=130° - мера второго угла.

Остальные два угла равны предыдущим, так как вертикальные.