В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)= =9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
=√3 см
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
=√147 см
Боковые грани правильной пирамиды это равные треугольники.
Сумма углов, прилежащих к боковой стороне, равна 180°
Меньший угол х, больший 3х, тогда х+2х=180
х=180/3
х=60
Меньший угол 60°, больший 2*60°=120°
Если опустить перпендикуляры из вершин тупых углов на большую сторону, то отрезки, отсекаемые ими равны половинам боковых сторон, т.к. прямоугольные треугольники, образованные высотами, боковыми сторонами и отрезками нижнего большего содержат угол в 30°, против которого лежат эти отрезки, т.е. 8/2=4/см/
а нижнее большее основание состоит из меньшего основания и двух отрезков по 4+4+4=12.
Периметр - сумма длин всех сторон, он равен
4+12+2*8=32/см/
средняя линия трапеции равна полусумме оснований. т.е. (12+4)/2=
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)=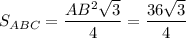 =9√3 см².
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)=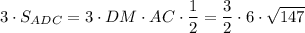 =9√147 см²
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².
Сумма углов, прилежащих к боковой стороне, равна 180°
Меньший угол х, больший 3х, тогда х+2х=180
х=180/3
х=60
Меньший угол 60°, больший 2*60°=120°
Если опустить перпендикуляры из вершин тупых углов на большую сторону, то отрезки, отсекаемые ими равны половинам боковых сторон, т.к. прямоугольные треугольники, образованные высотами, боковыми сторонами и отрезками нижнего большего содержат угол в 30°, против которого лежат эти отрезки, т.е. 8/2=4/см/
а нижнее большее основание состоит из меньшего основания и двух отрезков по 4+4+4=12.
Периметр - сумма длин всех сторон, он равен
4+12+2*8=32/см/
средняя линия трапеции равна полусумме оснований. т.е. (12+4)/2=
8/см/