1. Отрезок, для которого указано, какая из его граничных точек считается началом, а какая - концом, называется вектором. Нулевой вектор, проекция которого изображается в виде точки, так как его длинна равна нулю ( поэтому и можем изобразить только точкой) 5. Из точки можно построить только один равный вектор, так как они должны быть параллельны, одинаковой длины и направленности 6. Для любых векторов а, b, и с справедливы равенства: 1. a + b = b + a (переместительный закон) 2. (a + b) + c = a + (b + c) (сочетательный закон)
№1: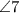 . №2:
. №2: 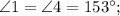
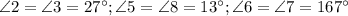 .
.
Объяснение:№1.
Пусть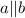 , тогда
, тогда  - секущая.
- секущая.
Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна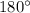 .
.
№2.
Обозначим данные прямые буквами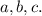
Пусть - секущая прямых
- секущая прямых  и
и 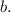
Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".
============================================================
Свойство: "Вертикальные углы равны".
Свойство: "Сумма смежных углов равна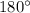 ".
".
Рассмотрим углы, образовавшиеся при пересечении прямых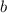 и
и 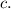
===========================================================
Рассмотрим углы, образовавшиеся при пересечении прямых и
и  .
.
5. Из точки можно построить только один равный вектор, так как они должны быть параллельны, одинаковой длины и направленности
6. Для любых векторов а, b, и с справедливы равенства:
1. a + b = b + a (переместительный закон)
2. (a + b) + c = a + (b + c) (сочетательный закон)