Площа трапеції дорівнює 32 см², а її висота дорівнює 8 см. Знайдіть основи трапеції, якщо одна з них на 4 см менша від другої. а) 54 см б) 64 см в) 56 см г) 112 см
Проведём от точки N к точке P отрезок PN и от точки M к точке O отрезок MO так, что MN - часть средней линии данной трапеции. Соответственно, исходя из этого условия и зная длины BC и AD найдём длину отрезка PO.
(см).
Вернёмся к условию задачи. M и N — СЕРЕДИННЫЕ точки диагоналей AC и BD трапеции ABCD. И следовательно из ранее сказанной записи "MN - часть средней линии данной трапеции" мы можем сказать, что PN и MO равны сумме BC.
(см).
Поскольку нам известен отрезок, на котором находится искомый отрезок MN и два составляющих по бокам отрезка PO, то найдём отрезок MN.
Проведём от точки N к точке P отрезок PN и от точки M к точке O отрезок MO так, что MN - часть средней линии данной трапеции. Соответственно, исходя из этого условия и зная длины BC и AD найдём длину отрезка PO.
Вернёмся к условию задачи. M и N — СЕРЕДИННЫЕ точки диагоналей AC и BD трапеции ABCD. И следовательно из ранее сказанной записи "MN - часть средней линии данной трапеции" мы можем сказать, что PN и MO равны сумме BC.
Поскольку нам известен отрезок, на котором находится искомый отрезок MN и два составляющих по бокам отрезка PO, то найдём отрезок MN.
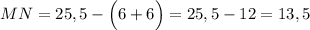 (см)
(см)
ответ:ответ: 28, 19,8
Объяснение:
1. Катет, лежащий напротив угла в 30 градусов равен половине гипотенузы. Следовательно, гипотенуза DE=DF*2=14*2=28 см
2. Угол А= 90- угол В=90-60=30. Катет, лежащий против угла в 30 градусов равен половине гипотенузы. ВС=38/2=19 см
3. ΔКРЕ: ∠Р = 90°, ∠К = 60°, ⇒ ∠Е = 30°.
ΔРКМ: ∠КРМ = 90°, ∠КМР = 60°, ⇒ ∠МКР = 30°.
∠PKM = 30°.
∠РКЕ = 60°,
∠EKM = ∠РКЕ - ∠1 = 60° - 30° = 30°.
Тогда треугольник КМЕ равнобедренный (∠PEK = ∠EKM = 30°),
КМ = МЕ = 16 см
В прямоугольном треугольнике РКМ напротив угла в 30° лежит катет, равный половине гипотенузы, т.е.
РМ = 1/2 КМ = 8 см