1)Два треугольника называются подобными, если их углы соответственно равны
1) да ; 2) нет
Вспомним 1-й признак подобия:
если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2)Любые два прямоугольных и равнобедренных треугольника подобны.
1) нет ;2) да
Верно. По первому признаку. Углы при основании равны 45°,а напротив основания 90°
3)Любые два прямоугольных треугольника подобны.
1) да 2) нет
В таких треугольниках мы можем утверждать только о равенстве одного угла-прямого. Ни для одного признака подобия этого недостаточно
Неверно
4 )Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны
1) да 2) нет
Более подходящие признаки
2-й -если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны. Равенство углов нам не дано. Утверждать не можем
3-й -: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны. Нам даны по 2 стороны. Утверждать не можем
5)Если два треугольника подобны, то их соответствующие стороны равны
1) да; 2) нет
3-й признак: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны.
6)Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
1) да ; 2) нет
Теорема верная.
7)Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.
1) да ; 2) нет
Это первый признак равенства. А,равные треугольники подобны
8)Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны.
1) да ; 2) нет
Вспомним 1-й признак подобия:
если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их и
Проведём диагональ в квадрате и диагональ в квадрате
Рассмотрим .
У квадрата все углы прямые.
, по свойству квадрата.
, так как диагонали квадрата делят углы пополам.
по 1 признаку подобия треугольников.
4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
1)Два треугольника называются подобными, если их углы соответственно равны
1) да ; 2) нет
Вспомним 1-й признак подобия:
если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2)Любые два прямоугольных и равнобедренных треугольника подобны.
1) нет ;2) да
Верно. По первому признаку. Углы при основании равны 45°,а напротив основания 90°
3)Любые два прямоугольных треугольника подобны.
1) да 2) нет
В таких треугольниках мы можем утверждать только о равенстве одного угла-прямого. Ни для одного признака подобия этого недостаточно
Неверно
4 )Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны
1) да 2) нет
Более подходящие признаки
2-й -если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны. Равенство углов нам не дано. Утверждать не можем
3-й -: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны. Нам даны по 2 стороны. Утверждать не можем
5)Если два треугольника подобны, то их соответствующие стороны равны
1) да; 2) нет
3-й признак: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны.
6)Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
1) да ; 2) нет
Теорема верная.
7)Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.
1) да ; 2) нет
Это первый признак равенства. А,равные треугольники подобны
8)Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны.
1) да ; 2) нет
Вспомним 1-й признак подобия:
если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Всё в разделе "Объяснение".
Объяснение:1. Неверно.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их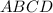 и
и 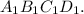
Проведём диагональ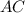 в квадрате
в квадрате 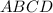 и диагональ
и диагональ 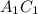 в квадрате
в квадрате 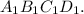
Рассмотрим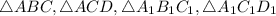 .
.
У квадрата все углы прямые.4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.