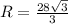Площина а паралельна стороні ВС трикутника ВСД та перетинає сторони ВД і СД в точках В1 і С1. Знайдіть довжину сторони СД, якщо В1 С1 =2 см. ВС= 8 см. СС1 = 3 см. (малюнок є)
Нарисовал чертеж с обозначениями. Во-первых, описать окружность можно только около равнобедренной трапеции. Надо найти радиус этой окружности. Заметим, что окружность эта описана как около трапеции ABCD, так и около треугольника ABD.
Для треугольника ABD воспользуемся теоремой синусов и получим
То есть
Даже вот так. Радиус этой окружности равен длине стороны BD.
Осталось лишь её найти. Раз трапеция равнобедренная, то и прямоугольные треугольники ABH и DCK равны (по катету - высоте и гипотенузе - боковой стороне трапеции). Значит, AH = KD
Тогда AD = AH + HK + KD = 2*AH + HK
BCKH - прямоугольник, BC = HK = 12
AH = 0.5 * (AD - HK) = 0.5 * (20 - 12) = 4
HD = HK + KD = 12 + 4 = 16
Не хватает стороны BH. Её можно найти из треугольника ABH
А) треугольник BOC=BOA( по 2 признаку рав треугольников,BO-общая сторона,АO=OC(по условию)угол BOC=BOA( по условию)В равных треугольниках соответственные элементы равны AB=BC поэтому треугольник ABC равнобедренный в равнобедренных треугольниках углы при основании равны BAC=BCA б) проведем прямую BM проходящую через точку О и прямую AC. треугольник AOM=MOC (по 2 признаку равенства треугольников, OM-общая сторона ,AO=OC и уголы OMA=OMC)В равных треугольниках соответсвующие элементы равны. AM=MC отсюда следует продолжение BO проходит через середину AC
Нарисовал чертеж с обозначениями. Во-первых, описать окружность можно только около равнобедренной трапеции. Надо найти радиус этой окружности. Заметим, что окружность эта описана как около трапеции ABCD, так и около треугольника ABD.
Для треугольника ABD воспользуемся теоремой синусов и получим
То есть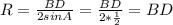
Даже вот так. Радиус этой окружности равен длине стороны BD.
Осталось лишь её найти. Раз трапеция равнобедренная, то и прямоугольные треугольники ABH и DCK равны (по катету - высоте и гипотенузе - боковой стороне трапеции). Значит, AH = KD
Тогда AD = AH + HK + KD = 2*AH + HK
BCKH - прямоугольник, BC = HK = 12
AH = 0.5 * (AD - HK) = 0.5 * (20 - 12) = 4
HD = HK + KD = 12 + 4 = 16
Не хватает стороны BH. Её можно найти из треугольника ABH
Теперь по теореме Пифагора ищем BD
ответ: