Площина бетта перетинає сторони ав і ас трикутника авс у точках n і d відnовідно та паралельна стороні вс, аd=6 см, dn: св- 3: 4. знайдіть довжину сторони ас трнкутника.
Користуючись лемою про подібні трикутники, можна сказати, що трикутник ADN ~ трикутнику ACB, так як пряма DN || прямій CB. Відповідно AD:AC=DN:CB=3:4 =>
У треугольников AND и ABC угол А - общий и ∠AND = ∠ABC
как соответственные углы при ND ║ BC и секущей AB,
следовательно, ΔAND ~ ΔABC. Из подобия треугольников
следует, что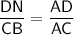
ответ: 8 см.
Відповідь: AC=8 см
Пояснення:
Користуючись лемою про подібні трикутники, можна сказати, що трикутник ADN ~ трикутнику ACB, так як пряма DN || прямій CB. Відповідно AD:AC=DN:CB=3:4 =>
=> так як AD=6 см, то 6:AC=3:4=>
=> 3×AC=24 => AC=8 см.