2. уравнение прямой: y=kx+C; Эта прямая пересекает ось 0Y в точке C, а тангенс угла между этой прямой и осью 0X равен k.
Если прямая параллельна оси 0X, то угол между прямой и этой осью равен нулю. Тангенс нуля тоже равен нулю, значит k=0. Получаем уравнение прямой, параллельной оси 0X: y=0*x+C; то есть y=C
Значит в задании 2. уравнение прямой имеет вид y=-2
3. подставляем значение абсциссы (x=1) в уравнение и находим нужные точки.
Первая точка (1;4) вторая (1;-4)
4. уравнение окружности
Где (a;b) координаты центра окружности.
В данном уравнении
центр окружности находится в начале координат (0;0), значит наша прямая совпадает с осью 0Y и описывается уравнением x=0
5. прямая y=8 параллельна оси абсцисс 0X, значит диаметр окружности равен 8, а радиус равен 4.
1) а не параллельно b, т.к. угол4=180-60=120градусов (т.к. угол3 и угол4 смежные)
угол4 и угол 1 являются накрест лежащими, но они не равны, значит а не параллельна b.
2) угол3+угол4=180градусов, т.к. они односторонние.
пусть угол3=х, тогда угол4=х+30
х+х+30=180
2х=150
х=75 градусов (это угол3)
75+30=105градусов (это угол4)
3) рассмотрим треугольники ЕСМ и МВД. У них: ЕМ=МВ по условию, СМ=МД по условию, уголЕМС=углуДМВ т.к. они вертикальные. Значит, треугольникЕСМ=треугольникуМВД по I признаку. => ЕС=ВД.
не понятно, что там требуется доказать, если их параллельность, то тогда следующее:
Из равенства треугольников следует, что уголЕСМ=углуМДВ, а они являются накрест лежащими для ЕС и ВД и секущей СД. Следовательно, ЕС II ВД.
4) уголСДМ=углуМДК=68:2=34градуса, т.к. ДМ бисектриса.
уголСДМ=углуДМК=34градуса, т.к. они накрест лежащие для СД II МК и секущей ДМ.
смотри ниже
Объяснение:
2. уравнение прямой: y=kx+C; Эта прямая пересекает ось 0Y в точке C, а тангенс угла между этой прямой и осью 0X равен k.
Если прямая параллельна оси 0X, то угол между прямой и этой осью равен нулю. Тангенс нуля тоже равен нулю, значит k=0. Получаем уравнение прямой, параллельной оси 0X: y=0*x+C; то есть y=C
Значит в задании 2. уравнение прямой имеет вид y=-2
3. подставляем значение абсциссы (x=1) в уравнение и находим нужные точки.
Первая точка (1;4) вторая (1;-4)
4. уравнение окружности
Где (a;b) координаты центра окружности.
В данном уравнении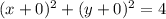
центр окружности находится в начале координат (0;0), значит наша прямая совпадает с осью 0Y и описывается уравнением x=0
5. прямая y=8 параллельна оси абсцисс 0X, значит диаметр окружности равен 8, а радиус равен 4.
1) а не параллельно b, т.к. угол4=180-60=120градусов (т.к. угол3 и угол4 смежные)
угол4 и угол 1 являются накрест лежащими, но они не равны, значит а не параллельна b.
2) угол3+угол4=180градусов, т.к. они односторонние.
пусть угол3=х, тогда угол4=х+30
х+х+30=180
2х=150
х=75 градусов (это угол3)
75+30=105градусов (это угол4)
3) рассмотрим треугольники ЕСМ и МВД. У них: ЕМ=МВ по условию, СМ=МД по условию, уголЕМС=углуДМВ т.к. они вертикальные. Значит, треугольникЕСМ=треугольникуМВД по I признаку. => ЕС=ВД.
не понятно, что там требуется доказать, если их параллельность, то тогда следующее:
Из равенства треугольников следует, что уголЕСМ=углуМДВ, а они являются накрест лежащими для ЕС и ВД и секущей СД. Следовательно, ЕС II ВД.
4) уголСДМ=углуМДК=68:2=34градуса, т.к. ДМ бисектриса.
уголСДМ=углуДМК=34градуса, т.к. они накрест лежащие для СД II МК и секущей ДМ.
уголДКМ=180-34-34=112градусов (т.к. сумма углов треугольника =180градусов)