По рис. 11 докажите, что ae=cd, если ab=bc.

Дано:

параллелепипед ABCDA1B1C1D1

AC = A1C1 = 6 см

BD = B1D1 = 8 см

AA1 = DD1 = CC1 = DD1 = 7 см

1. Рассмотрим ромб ABCD, лежащий в основании. По свойствам ромба, его диагонали пересекаются под прямым углом и точкой пересечения делятся попопам. Обозначим точку пересечения как O.

2. Рассмотрим треугольник AOD. Он прямоугольный, его катеты AO и OD.

AO = AC/2 = 6/2 = 3 см

OD = BD/2 = 8/2 = 4 см

Найдем гипотенузу AD:

AD =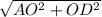 

AD = 5 см

3. Стороны ромба равны, значит, треугольник AOD = AOB = BOC = COD, AB = BC = CD = AD = 5 см. 

4. Теперь мы знаем все грани и можем найти площади.

Площадь оснований (площади ромбов) ABCD и A1B1C1D1 рассчитываются по формуле:

S = (AD * BC)/2 = 24 кв.см

Площади граней (всех в силу равенства сторон) -  как площади прягоугольников.

S = AA1 * AB = 7 * 5 = 35 кв.см

5. Площадь полной поверхности:

S = 2 * 24 + 4 * 35 = 48 + 140 = 188 кв.см

ответ: S = 188 кв.см

Вот и все :) Удачи!

Прямоугольный треугольник с катетам 4 см вписан в окружность. найдите площадь правильного шестиугольника, описанного около данной окружности.

Объяснение:

Дано : ΔАВС вписан в окружность, ∠С=90° , СА=СВ=4 см, правильный  шестиугольник описан  около данной окружности.

Найти :S(правильного шестиугольника).

Решение .

ΔАВС-прямоугольный, ∠С=90° , значит опирается на дугу в 180°⇒АВ диаметр. Найдем гипотенузу АВ по т. Пифагора

АВ=√( 4²+4²)=2√2 (см). Поэтому R=1/2*АВ=√2 (см).

Шестиугольник описан около данной окружности , значит для него √2 является радиусом вписанной окружности  r=√2 cм.

По формуле r₆= ( a₆√3) /2   ⇒   √2=( a₆√3) /2  или a₆=(2√2) /√3 (см)

S=1/2*Р*r

S=1/2*(6*(2√2) /√3 )*√2=12/√3=4√3 (cм²)