@ 319. через гипотенузу АВ равнобедренного прямоугольного треугольника- ка АВС под углом в 45° к его плоскости проведена плоскость расстояния от вершины прямого угла С на (рис. 326). Найдите площадь треугольника АВС[email protected]
Объяснение:
Т.к. проведена " плоскость на расстояния от вершины прямого угла С ", то СС₁⊥ γ ⇒Δ СС₁D-прямоугольный , sin45°=СС₁/DC , ,DС=L√2.
Т.к.ΔАВС-равнобедренный, прямоугольный , то ∠А=∠В=45°⇒ΔACD-равнобедренный ⇒AD=DС=L√2.
Из правильного треугольника АВС: из теоремы Пифагора: высота ВК равна 3 корня из 2. Угол ОАК - это угол между плоскостью АОС и основанием. Поскольку угол ОАК = 30 градусов, то катет ОК равен гипотенузы ОА как катет, который лежит против угла 30 градусов. ОК = ОА/2. Пускай ОК = х, тогда ОА = 2х. Из прямоугольного треугольника ОАК: за теоремой Пифагора: OA^2 = OK^2 + AK^2, 4x^2 = 9 - x^2, 3x^2 = 9, x^2 = 3, x = корень из 3. OK = корень из 3. Объем призмы равен площади основания умножить на высоту: S = So*H = S(ABC)*OK = BK*AC/2*OK = 9 корней из 6.
@ 319. через гипотенузу АВ равнобедренного прямоугольного треугольника- ка АВС под углом в 45° к его плоскости проведена плоскость расстояния от вершины прямого угла С на (рис. 326). Найдите площадь треугольника АВС[email protected]
Объяснение:
Т.к. проведена " плоскость на расстояния от вершины прямого угла С ", то СС₁⊥ γ ⇒Δ СС₁D-прямоугольный , sin45°=СС₁/DC ,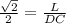
,DС=L√2.
Т.к.ΔАВС-равнобедренный, прямоугольный , то ∠А=∠В=45°⇒ΔACD-равнобедренный ⇒AD=DС=L√2.
И ΔВCD-равнобедренный ⇒ВD=DС=L√2.
Значит АВ=2L√2.
S=1/2*a*h , S(АВС)=1/2*2L√2*L√2=2L² .