Чтобы найти координаты вектора XY для точек X(x1,x2,x3) и Y(y1,y2,y3) нужно переместить X в 0, т.е просто отнять x1 из y1 и т.д. Итого XY(y1-x1, y2-x2, y3-x3). Аналогично вычисляем:
AB(1-2,-2-4,3-5)=AB(-1,-6,-2)
BC(-1-1,-2-(-2),4-3)=BC(-2,0,1)
AC(-1-2,-2-4,4-5)=AC(-3,-6,1)
Вектор XY*k получается домножением каждой координаты на k, чтобы вычесть вектора нужно из координат первого вектора вычесть координаты второго вектора:
Соединив центры K и М окружностей
между собой и каждый из них с точкой
касания, получим два треугольника с
общей вершиной в точке А на отрезке между
точками касания окружностей с прямой.
Радиус, проведенный к касательной
в точку касания, перпендикулярен ей
( свойство),
Получившиеся прямоугольные треугольники
подобны по равным вертикальным углам и
накрестлежащим у их центров.
Пусть радиус меньшей окружности будет r,
а большей - R, и пусть часть отрезка между
их точками касания у меньшей окружности
будет х.
Тогда отрезок у большей окружности 5-х
( см. рисунок)
Тогда из подобия треугольников следует
отношение:
r:R=x:(5-x)
4:8=x:(5-x)
8х=20-4x
12x=20
х=5/3- длина отрезка у меньшей окружности
5-5/3=10/3 длина отрезка у большей
окружности
По т.Пифагора
KA2=42+(5/13)2
KA2=16+25/9=169/9
KA=13/3
Из треугольника в большей окружности
MA2=82+(10/3)2=676/9
MA=26/3
KA+MA=13/3+26/3=39/3=13
KM=13 см
наверное так
а)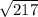
б)-28
Объяснение:
Чтобы найти координаты вектора XY для точек X(x1,x2,x3) и Y(y1,y2,y3) нужно переместить X в 0, т.е просто отнять x1 из y1 и т.д. Итого XY(y1-x1, y2-x2, y3-x3). Аналогично вычисляем:
AB(1-2,-2-4,3-5)=AB(-1,-6,-2)
BC(-1-1,-2-(-2),4-3)=BC(-2,0,1)
AC(-1-2,-2-4,4-5)=AC(-3,-6,1)
Вектор XY*k получается домножением каждой координаты на k, чтобы вычесть вектора нужно из координат первого вектора вычесть координаты второго вектора:
a=3AB-4AC=(3*(-1)-4*(-3),3*(-6)-4*(-6),3*(-2)-4*1)=(9,6,-10)
Длина вектора a - среднее квадратичное его координат:
|a|=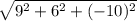 =
=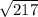
Формула скалярного произведения векторов a(a1,a2,a3) и b(b1,b2,b3) - ab=a1*b1+a2*b2+a3*c3
Итого ab=9*(-2)+6*0+(-10)*1=-28