Две прямые, перпендикулярные одной и той же плоскости, параллельны.
PP1 ⊥ ,
QQ1 ⊥ => PP1 II QQ1
Через 2 параллельные прямые можно провести плоскость и притом только одну .
PP1 и QQ1 принадлежат одной плоскости B.
Пусть P1Q1 - линия пересечения плоскостей Альфа и Бета.
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Задача 1
угол АВС= 180- угол КВС=180-108=72°(т.к смежные углы в сумме дают 180°)
угол ВСА=180- угол ВСD= 180-137=43°(т.к смежные углы в сумме дают 180°)
угол А=180- угол АВС- угол ВСА=180-72-43=65°(сумма всех углов в треугольнике равна 180°)
ответ:65; 72;43
Задача 2
внешний угол равен сумме двух противоположных внутренних
Угол С= угол А + угол В
145=3х+17+7х+28
-10х=-100
х=10
Угол А = 3х+17°=30+17=47°
ответ:47°
Задача 3
Угол А внешний= углу САВ=60° (т.к вертикальные)
Угол В=180- угол САВ - -уголС=180-60-90=30
Опустим высоту СК
т.к угол В=30°, то СК=1/2ВС=3,9(т.к катет лежащий против 30° равен половине гипотенузы)
ответ: 30; 3,9
PP1Q1Q-квадрат
Периметр равен 41,2 см
Объяснение:
Две прямые, перпендикулярные одной и той же плоскости, параллельны.PP1 ⊥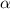
,
QQ1 ⊥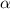
=> PP1 II QQ1
Через 2 параллельные прямые можно провести плоскость и притом только одну .PP1 и QQ1 принадлежат одной плоскости B.
Пусть P1Q1 - линия пересечения плоскостей Альфа и Бета.
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.=>PQ II P1Q1
PQQ1P1 - параллелограмм.
Так как < PP1Q1, <QQ1P1 равны 90°, то
PQQ1P1 - прямоугольник.
PP1=PQ => PQQ1P1 - квадрат.
Периметр квадрата находится по формуле:
Р=4а=4×10,3= 41,2 см