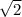Посчитайте примеры 1/2а^2+а^2=

Поскольку наклонные равны, значит и их проекции будут равны между собой. Далее, если рассмотреть треугольник, который составляют наклонные, то он правильный, поэтому если проекция наклонной равняется Х, то сторона этого треугольника будет равняться Х* . После, если рассмотреть треугольник, который составляет наклонная и ее проекция, то мы видим, что он прямой. В нем мы знаем величину катета и гипотенузы, поэтому сейчас необходимо доказать, что этот треугольник - равнобедренный. Поскольку гипотенуза что в данном треугольнике, что в предыдущем рассмотренном равна, а так же равен один из катетов, мы делаем вывод, что второй катет так же равен (из равенства прямоугольных треугольников). Поэтому, в равнобедренном треугольнике, где угол при вершине - прямой, остальные углы равняются по 45 градусов.

2 Периметр десятого четырехугольника равен 1,1 (1,125). Наблюдается геометрическая прогрессия, уменьшения площадей четырехугольников: площадь третьего меньше первого в 2 раза, 5-того в 2 раза меньше 3-го и т.д., аналогично и с четными четырехугольниками: Площадь четвертого меньше второго в 2 раза.  Находим 5 четный член прогрессии по формуле (это и есть площадь 10 четырехугольника) b5=b1/gСтепень(5-1); Периметр b1 вычисляем начертив второй четырехугольник P=18см. Р=18/2 в степень(5-1)=18/16=1,125 см                                     1 Периметр первого равен 26 см Найдем периметр 9-того четырехугольника, это пятый в геометрической последовательности нечетных четырехугольников: Р=26/2 в степени(5-1). Р26/16=1.6 см