Посогите ! найдите углы четырёхугольника abcd, и градусные меры дуг ab, bc, cd, ad, если bd-диаметр окружности с центром о, а хорда ас делит пополам радиус ов и перпендикуляра к нему.
Так как треугольник ABC - равносторонний и равнобедренный, то высота в нем является медианой и биссектрисой, значит AH=27√3. Основание AC. Далее рассмотрим треугольник ABH - прямоугольный. По теореме Пифагора находим BH:
BH=81
1706.
Так как треугольник ABC - равносторонний и равнобедренный, то высота в нем является медианой и биссектрисой, значит AH=23√3. Основание AB. Далее рассмотрим треугольник ACH - прямоугольный. По теореме Пифагора находим CH:
CH=69
1711.
Так как треугольник ABC - равнобедренный, то угол B и угол C равны по 30 градусов. Рассмотрим один из двух треугольников ABH - прямоугольный. По свойству мы знаем, что катет лежащий против угла в 30 градусов равен половине гипотенузы, отсюда следует, что:
Проведем высоту из меньшего основания так чтобы получили прямоугольный треугольник, у этого прямоугольного треугольника гиппотенуза= 2√3
Т.к угол равен 120 градусов, то угол треугольника = 120-90=30 , а против угла в 30 градусов лежит катет равный половине гипотенузы и он равен √3=> большее основание = 6+√3
по теореме Пифагора находим третью сторону треугольника х=√4*3-3= 3
Площадь трапеции= полусумма оснований умноженная на высоту=>
1704.
Так как треугольник ABC - равносторонний и равнобедренный, то высота в нем является медианой и биссектрисой, значит AH=27√3. Основание AC. Далее рассмотрим треугольник ABH - прямоугольный. По теореме Пифагора находим BH:
BH=81
1706.
Так как треугольник ABC - равносторонний и равнобедренный, то высота в нем является медианой и биссектрисой, значит AH=23√3. Основание AB. Далее рассмотрим треугольник ACH - прямоугольный. По теореме Пифагора находим CH:
CH=69
1711.
Так как треугольник ABC - равнобедренный, то угол B и угол C равны по 30 градусов.
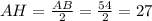
Рассмотрим один из двух треугольников ABH - прямоугольный.
По свойству мы знаем, что катет лежащий против угла в 30 градусов равен половине гипотенузы, отсюда следует, что:
AH=27
120 градусов это угол при меньшем основании
Проведем высоту из меньшего основания так чтобы получили прямоугольный треугольник, у этого прямоугольного треугольника гиппотенуза= 2√3
Т.к угол равен 120 градусов, то угол треугольника = 120-90=30 , а против угла в 30 градусов лежит катет равный половине гипотенузы и он равен √3=> большее основание = 6+√3
по теореме Пифагора находим третью сторону треугольника х=√4*3-3= 3
Площадь трапеции= полусумма оснований умноженная на высоту=>
S=(12+√3)\2 *3=(36+3√3)2