Формула линейной функции имеет вид y=kx+b, где х — независимая переменная (абсцисса точки); y — зависимая переменная (ордината точки); k, b — числовые коэффициенты.
Числовой коэффициент b показывает, в какой точке график пересекает ось ординат (Оу). В данном случае b = 3. Наша формула обретет вид:
Числовой коэффициент k отвечает за наклон графика линейной ф-ции:
Если график ф-ции образует с положительной осью Ox острый угол, тогда коэффициент k > 0, если тупой — k < 0.
В данном случае k < 0, то есть k — отрицательное число.
Из формулы выразим k:
Возьмём любую удобную нам точку на прямой и подставим ее координаты в полученную формулу:
A (4; 0)
В итоге, формула линейной функции получится следующей:
Сумма острых углов прямоугольного треугольника составляет 90°, и сли <В=30°, то <А=90–30=60°. Так как AL биссектриса, то <CAL=<KAL=60÷2=30°. Kаждая. высота, проведённая в каждом треугольнике, образуют другие треугольники, которые являются прямоугольными. В прямоугольном треугольнике катет, лежащий напротив угла В=30°, равен половине гипотенузы, поэтому в ∆ALK LK=½×AL=16÷2=8. Катет KL также является катетом в ∆LKB и гипотенуза ВL в ∆ LKB будет больше в 2 раза больше чем KL, поэтому ВL=8×2=16. Рассмотрим ∆LKB. Если угол В=30°, то угол BLK=60°(90–30=60), а <LKM в ∆LKM=30°, и катет LM=½×KL=½×8=4. Если BL=16, то ВМ=BL–ML=16–4=12. В ∆BMN ВМ - гипотенуза, а MN меньший катет, лежащий напротив угла В=30°, и поэтому равен ½× ВМ, поэтому MN=12÷2=6
Формула линейной функции имеет вид y=kx+b, где х — независимая переменная (абсцисса точки); y — зависимая переменная (ордината точки); k, b — числовые коэффициенты.
Числовой коэффициент b показывает, в какой точке график пересекает ось ординат (Оу). В данном случае b = 3. Наша формула обретет вид:
Числовой коэффициент k отвечает за наклон графика линейной ф-ции:
Если график ф-ции образует с положительной осью Ox острый угол, тогда коэффициент k > 0, если тупой — k < 0.
В данном случае k < 0, то есть k — отрицательное число.
Из формулы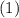
выразим k:
Возьмём любую удобную нам точку на прямой и подставим ее координаты в полученную формулу:
A (4; 0)В итоге, формула линейной функции получится следующей:
MN=6
Объяснение:
Сумма острых углов прямоугольного треугольника составляет 90°, и сли <В=30°, то <А=90–30=60°. Так как AL биссектриса, то <CAL=<KAL=60÷2=30°. Kаждая. высота, проведённая в каждом треугольнике, образуют другие треугольники, которые являются прямоугольными. В прямоугольном треугольнике катет, лежащий напротив угла В=30°, равен половине гипотенузы, поэтому в ∆ALK LK=½×AL=16÷2=8. Катет KL также является катетом в ∆LKB и гипотенуза ВL в ∆ LKB будет больше в 2 раза больше чем KL, поэтому ВL=8×2=16. Рассмотрим ∆LKB. Если угол В=30°, то угол BLK=60°(90–30=60), а <LKM в ∆LKM=30°, и катет LM=½×KL=½×8=4. Если BL=16, то ВМ=BL–ML=16–4=12. В ∆BMN ВМ - гипотенуза, а MN меньший катет, лежащий напротив угла В=30°, и поэтому равен ½× ВМ, поэтому MN=12÷2=6