Да, без этих формул задача требует применения извилин :))) На чертеже представлены простые вычисления этих радиусов из простого подобия треугольников. Справа от высоты вычисления радиуса вписанной окружности, в левой части риснка - радиуса описанной окружноти (точнее - диаметра:)).
Для начала следует понять, что АВС составлен из двух прямоугольных треугольников АВМ и ВМС, подобных "египетскому", со сторонами 9, 12, 15. То есть высота ВМ = 12.
1. О1 - центр вписанной окружности. О1К - радиус в точку касания. Из подобия треугольников ВМС и ВКО1 следует КО1/ВО1 = МС/ВС; при этом МО1 = КО1 = r;
r/(12 - r) = 3/5; r = 9/2;
2. Чтобы вычислить диаметр описанной окружности, для начала скажем, что центр её О лежит на ВМ. Продолжим ВМ до пересечения с описанной окружностью, пусть это точка Е (то есть ВЕ и есть диаметр D = 2*R). Тогда АЕ обязательно перпендикулярно АВ, так как вписанный в окружность угол ВАЕ опирается на диаметр ВЕ. Треугольники ЕАВ и АМВ прямоугольные и имеют общий угол АВМ. Поэтому они подобны, и ВЕ/АВ = АВ/ВМ.
Да, без этих формул задача требует применения извилин :))) На чертеже представлены простые вычисления этих радиусов из простого подобия треугольников. Справа от высоты вычисления радиуса вписанной окружности, в левой части риснка - радиуса описанной окружноти (точнее - диаметра:)).
Для начала следует понять, что АВС составлен из двух прямоугольных треугольников АВМ и ВМС, подобных "египетскому", со сторонами 9, 12, 15. То есть высота ВМ = 12.
1. О1 - центр вписанной окружности. О1К - радиус в точку касания. Из подобия треугольников ВМС и ВКО1 следует КО1/ВО1 = МС/ВС; при этом МО1 = КО1 = r;
r/(12 - r) = 3/5; r = 9/2;
2. Чтобы вычислить диаметр описанной окружности, для начала скажем, что центр её О лежит на ВМ. Продолжим ВМ до пересечения с описанной окружностью, пусть это точка Е (то есть ВЕ и есть диаметр D = 2*R). Тогда АЕ обязательно перпендикулярно АВ, так как вписанный в окружность угол ВАЕ опирается на диаметр ВЕ. Треугольники ЕАВ и АМВ прямоугольные и имеют общий угол АВМ. Поэтому они подобны, и ВЕ/АВ = АВ/ВМ.
2*R/15 = 15/12, R = 75/8;
В треугольнике АВС - проведем высоту ВВ1 ,высота в равнобедренном треугольнике явл. и биссектрисой, и медианой ->АВ1=1/2* АС=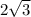 .
.
Угол А= углу С= (180-120):2=30
Рассмотрим треугольник АВВ1 - угол В1=90, а угол А =30 -> ВВ1=1/2*АВ(как катет лежащий против угла равоного 30 градусов).
Пусть АВ - Х см,тогда ВВ1 =1/2 Х см.По теореме Пифагора:
Отсюда х= 4
S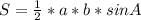
S(ABC)=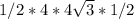 =
=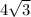 .
.
2)Обозначим середину АМ точкой L , а середину HC - т.О
Так МН - средняя линия труег АВС ,то МН = 1/2*АС=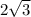 .
.
Теперь рассмотрим трапецию АМНС
Здесь LO явл. средней линией -> LO=1/2*(MH+AC)=1/2*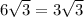 .
.