Геометрия: Построить симметричные фигуры .

Построить симметричные фигуры .

Показать ответ

Ответ:

JeepandChira13

08.01.2023 05:00

ответ:

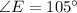
$\angle E=105^{\circ}$

Объяснение:

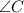Проведём биссектрисы $\angle B$ и $\angle C$ . Пусть они пересекаются в точке .

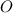Также проведём отрезки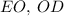 $EO, \: OD$ и .

========================================

Рассмотрим $\triangle BOC$ :

$\angle OBC = 140^{\circ}:2=70^{\circ}$ , т.к. - биссектриса.

$\angle OCB=110^{\circ}:2=55^{\circ}$ , т.к. - биссектриса.

Сумма внутренних углов треугольника равна $180^{\circ}$ .

$\Rightarrow \angle BOC=180^{\circ}-(70^{\circ}+55^{\circ})=180^{\circ}-125^{\circ}=55^{\circ}$

$\Rightarrow \triangle BOC$ - равнобедренный.

========================================

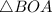Рассмотрим $\triangle BOA$ и $\triangle BOC$ :

$\angle ABO=\angle CBO$ , т.к. - биссектриса;

AB=CB (по условию); OB - общая сторона.

$\Rightarrow \triangle BOA=\triangle BOC$ (по I признаку равенства треугольников).

========================================

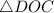Рассмотрим $\triangle BOC$ и $\triangle DOC$ :

$\angle BCO=\angle DCO$ , т.к. - биссектриса;

BC=CD (по условию), - общая сторона.

$\Rightarrow \triangle BOC=\triangle DOC$ (по I признаку равенства треугольников).

========================================

$\Rightarrow \triangle BOA=\triangle DOC$ , т.е. мы имеем три равных равнобедренных тр-ка:

$\boxed{\triangle BOA, \: \triangle DOC,\: \triangle BOC}$

========================================

Рассмотрим $\triangle EDO$ :

$\angle EDO=130^{\circ}-\angle ODC=130^{\circ}-70^{\circ}=60^{\circ}$ .

$\Rightarrow \triangle EDO$ - равносторонний $\Rightarrow FA=EO$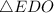

========================================

Рассмотрим геометрическую фигуру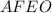 AFEO :

$\angle FAO=100^{\circ}-\angle OAB=100^{\circ}-55^{\circ}=45^{\circ}$ .

$\angle AOE=360^{\circ}-(55^{\circ}+55^{\circ}+55^{\circ}+60^{\circ})=135^{\circ}$ (т.к. в полном угле всего 360°)

При пересечении двух параллельных прямых секущей, сумма односторонних углов равна $180^{\circ}$ .

$\angle FAO+\angle EOA=180^{\circ} \Rightarrow FA|| EO$

Если у геометрической фигуры есть 4 угла, 4 стороны, а 2 стороны равны и параллельны, то этот четырёхугольник - параллелограмм.

У параллелограмма противоположные углы равны.

$\Rightarrow \angle FAO=\angle FEO=45^{\circ}$ .

$\Rightarrow \angle E=\angle FEO+\angle DEO=45^{\circ}+60^{\circ}=105^{\circ}$

========================================

В шестиугольнике ABCDEF выполнены равенства FA=AB=BC=CD=DE, ∠A=100∘, ∠B=140∘, ∠C=110∘, ∠D=130∘. Найд

0,0(0 оценок)

Ответ:

krioss

08.06.2022 14:41

Две прямые касаются окружности (радиусом 9 см) с центром О в точках Р и K и пересекаются в точке M. Найдите угол между этими прямыми, если ОМ = 18 см.

Объяснение:

Дано Окр О( R=9) , МР, МК-касательные , ОМ=18 см.

Найти ∠РМК.

Решение.

ΔРМО-прямоугольный, по свойству касательной. Т.к гипотенуза ОМ = 18 см, катет ОР =9 см в два раза меньше , то угол ∠РМО=30°.

Отрезки касательных к окружности, проведенных из одной точки М, равны и составляют равные углы ( это ∠РМО и ∠КМО ) с прямой, проходящей через эту точку и центр окружности ⇒∠РМО и ∠КМО.

Тогда ∠РМК=∠РМО + ∠КМО= 30°+30°=60°

ответ.∠РМК=60°

0,0(0 оценок)

Популярные вопросы: Геометрия