Построить треугольник по трем сторонам:
Первый треугольник:
а= 3,5 см; b= 5 см; с= 11 см

Объяснение:

Чтобы говорить об одном и том же параллелепипеде, я нарисовал рисунок и прикрепил его, переверните для удобства, а то фото неправильно загрузилось. Итак.

Большой диагональю параллелепипеда называется самая большая его диагональ, которая проходит сквозь всего его, на рисунке таких диагоналей можно построить целых 4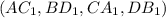 . Они все равны и я буду находить  .

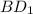Смотрим на него внимательно и видим, что если провести диагональ в основании BD, то получится прямоугольный треугольник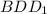 . У нас известен один из его катетов, а надо найти гипотенузу. Найдем катет BD. Он находится в свою очередь в другом прямоугольном треугольнике CBD, где известны оба катета, они равны 2 и 3. По теореме Пифагора:

Теперь применяем теорему Пифагора, чтобы найти диагональ:

Треугольник — три угла,

Посмотрите детвора:

Три вершины очень острых —

Треугольник — «остроносый».

Стороны в нем тоже три:

Раз, два, три — ты посмотри.

Треугольник мы рисуем,

Знать теперь его мы будем.

***

Треугольник мой любимый,

Ты сегодня прям красивый.

Равнобедренный ты мой,

Ты пойдешь играть со мной?

Медиана из вершины,

Зло бросаясь, без причины.

Делит сторону напротив,

Пополам, как между прочим!

Треугольника высОты

Не скучают без работы,

Пересёкшись, чтоб мы знали,

Ортоцентр сим создали.

В треугольниках, без слов,

Центры вписанных кругов —

Выявляют, вне сомнения,

Биссектрис пересечения.

Центром тяжести зовётся

Медиан пересечение.

Даже Карлсон сознаётся:

«Треугольник — не печенье!»

Чтобы в круг вписался он

К серединам трёх сторон,

Строго под прямым углом,

Мы прямые проведём…

Пересечения их точка

Искомый центрик для кружочка!

Объяснение: