Постройте окружность, возьмите точку b вне окружности, проведите касательные к окружности и измерьте радиус, отрезки касательных и расстояние от центра окружности до точки b. проверьте, выполняется ли теорема пифагора
Внешний угол правильного многоугольника и его внутренний угол являются смежными, значит, их сумма равна 180°.
Т.к. по условию задачи внутренний угол в 8 раз больше внешнего, то пусть внешний угол х°, тогда внутренний угол будет равен (8х)° (см. рис.). Составим и решим уравнение:
Зная 2 стороны и угол между ними, мы можем найти третью сторону — по теореме косинусов.
Косинус бетты мы найдём по её синусу:
β = 45°.
Теперь, чтобы найти третью сторону — используем теорему косинусов:
Теперь, зная все стороны треугольника, найдём площадь — по теореме Герона:
Вывод: S = 20.56.
2.
Для вычисления синуса альфы, нам потребуется знать косинус альфы, а для вычисления этого же косинуса, нам и сторон достаточно — используем теорему косинусов:
Этим следует:
Вывод: sinα = 0.92.
3.
Найдём синус гаммы:
Формула вычисления площади, через 2 стороны и синус — такова:
Внешний угол правильного многоугольника и его внутренний угол являются смежными, значит, их сумма равна 180°.
Т.к. по условию задачи внутренний угол в 8 раз больше внешнего, то пусть внешний угол х°, тогда внутренний угол будет равен (8х)° (см. рис.). Составим и решим уравнение:
х + 8х = 180.
9х = 180,
х = 180 : 9,
х = 20.
Значит, внутренний угол правильного многоугольника равен
8 · 20° = 160°.
Внутренний угол правильного многоугольника находят по формуле:
180° · (n - 2) / n, где n - число сторон правильного многоугольника.
Имеем:
180° · (n - 2) / n = 160°,
180° · (n - 2) =160° · n,
9 · (n - 2) = 8 · n,
9n - 18 = 8n,
9n - 8n = 18,
n = 18.
Значит, наш правильный многоугольник имеет 18 сторон.
ответ: 18 сторон.
1.
Зная 2 стороны и угол между ними, мы можем найти третью сторону — по теореме косинусов.
Косинус бетты мы найдём по её синусу:
β = 45°.
Теперь, чтобы найти третью сторону — используем теорему косинусов:
Теперь, зная все стороны треугольника, найдём площадь — по теореме Герона:
Вывод: S = 20.56.
2.
Для вычисления синуса альфы, нам потребуется знать косинус альфы, а для вычисления этого же косинуса, нам и сторон достаточно — используем теорему косинусов:
Этим следует:
Вывод: sinα = 0.92.
3.
Найдём синус гаммы:
Формула вычисления площади, через 2 стороны и синус — такова: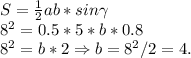
Вывод: AC = 4.