Правильная треугольная пирамида РАВС с высотой РН = 8см и стороной основания АВ = 12√3 рассечена плоскостью А1В1С1 , проходящей через середину Н1 высоты РН параллельно основанию АВС. Найти площадь боковой поверхности полученной усеченной пирамиды.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Следовательно, основание АС делится на два равных отрезка АН и НС, и угол ВНС является прямым. Мы получаем два прямоугольных треугольника, у которых все три стороны равны: АВ = ВС, т.к. треугольник равнобедренный по условию; АН = НС, т.к. ВН - медиана; ВН - общая сторона По третьему признаку равенства треугольников (если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны) наши треугольники АВН и ВНС равны.
Годится и второй признак равенства треугольников: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. В нашем случае: АВ = ВС по условию; угол А равен углу С, т.к. углы при основании равнобедренного треугольника равны; угол АВН равен углу СВН, т.к. ВН - биссектриса
Первый признак равенства треугольников тоже подходит: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. В нашем случае: АВ = ВС по условию АН = НС, т.к. ВН - медиана угол А равен углу С, т.к. в равнобедренном треугольнике углы при основании равны.
Объяснение:
Радиус окружности, описанной около правильного треугольника со стороной а определяется по формуле :
А радиус окружности вписанной в правильный треугольник со стороной а можно найти по формуле :
Значит радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной окружности . Так как по условию
R=8 см, то r =8:2=4 см.
Найдем длину окружности по формуле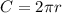
, где r -радиус окружности, вписанной в правильный треугольник, т.е. r =4 см.
Если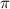
считать приближенно равным 3,14, то
С≈ 8*3,14=25,12 см.
Мы получаем два прямоугольных треугольника, у которых все три стороны равны:
АВ = ВС, т.к. треугольник равнобедренный по условию;
АН = НС, т.к. ВН - медиана;
ВН - общая сторона
По третьему признаку равенства треугольников (если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны) наши треугольники АВН и ВНС равны.
Годится и второй признак равенства треугольников: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. В нашем случае:
АВ = ВС по условию;
угол А равен углу С, т.к. углы при основании равнобедренного треугольника равны;
угол АВН равен углу СВН, т.к. ВН - биссектриса
Первый признак равенства треугольников тоже подходит: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. В нашем случае:
АВ = ВС по условию
АН = НС, т.к. ВН - медиана
угол А равен углу С, т.к. в равнобедренном треугольнике углы при основании равны.
Выбирай любой на свой вкус.