В равнобедренной трапеции диагональ является биссектрисой острого угла. Меньшее основание трапеции равно 17 см, а высота – 15 см. Чему равна площадь трапеции?
Объяснение:
1) АС-биссектриса ⇒ ∠ВАС=∠САD (*) .
Тк. ВС||AD, АС-секущая , то ∠САD=∠АСВ(**) как накрест лежащие.
Учтем (*) и (**) , получим ∠ВАС=АСВ ⇒ ΔАВС-равнобедренный и значит АВ=ВС= 17 см.
2) Пусть ВН ⊥AD, тогда ΔАВН-прямоугольный , по т. Пифагора АН=√(17²-15²)=8 (см) . По свойству равнобедренной трапеции
В равнобедренной трапеции диагональ является биссектрисой острого угла. Меньшее основание трапеции равно 17 см, а высота – 15 см. Чему равна площадь трапеции?
Объяснение:
1) АС-биссектриса ⇒ ∠ВАС=∠САD (*) .
Тк. ВС||AD, АС-секущая , то ∠САD=∠АСВ(**) как накрест лежащие.
Учтем (*) и (**) , получим ∠ВАС=АСВ ⇒ ΔАВС-равнобедренный и значит АВ=ВС= 17 см.
2) Пусть ВН ⊥AD, тогда ΔАВН-прямоугольный , по т. Пифагора АН=√(17²-15²)=8 (см) . По свойству равнобедренной трапеции
АН=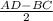
, 8 = 
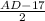, 16=AD-17 , AD=33 см .
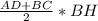S=
, S=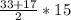 
= 25*15=375 (cм²) .
қиық пирамида көлемі
V=7√3 /36 см³
а2=2см
а1=1 см
α=30°
V- ?
қиық пирамида төменгі табанындағы дұрыс үшбұрыштың сырттай сызылған шеңбердің радиусы
Rт=a2/√3=2/√3 см
жоғарғы
Rж=а1/√3=1/√3 см
пирамида қиылмаған жағдайдағы биіктігі (пирамида төбесінен төмендегі табанға дейінгі )
Hтөм= tgα×Rт=tg30° ×2/√3=√3/3 × 2/√3=2/3 см
жоғарғы табан биіктігі
Hжоғ=tgα×Rж=tg30°×1/√3 =√3/3 × 1/√3=1/3 см
қиылған пирамида биіктігі
Hқ=Нтөм- Нжоғ=2/3 - 1/3 = (2 - 1)/3=1/3 см
жоғарғы табан ауданы ( дұрыс тең қабырғалы үшбұрыштың ауданы формуласымен )
S1=a²√3 /4= 1² ×√3 /4= √3 /4 см²
төменгі табан ауданы
S2=а²√3 /4=2²×√3 /4= 4×√3 /4=√3 см²
қиық пирамида көлемі
V=1/3 × H×(S1+√S1×S2 + S2)
V=1/3 × 1/3×(√3/4 + √(√3/4 × √3) + √3 )=
=1/9×(√3 /4 +√3 /2 + √3)=1/9×( (√3 +2√3 + 4√3)/4 )=
=1/9 × 7√3/ 4=7√3 /36 см³