Принимаю решения от пользователей,не менее чем со статусом умный! ! даны координаты вершин четырехугольника abcd: а (–6; 1), в (0; 5), с (6; –4), d (0; –8). докажите, что abcd – прямоугольник, и найдите координаты точки пересечения его диагоналей.
По признаку параллелограмма (если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам - то он параллелограмм), делаем вывод, что ABCD - параллеллограмм
По формуле расстояний между двумя точками, задаными координатами
находим длины диагоналей AC и BD
Диагонали равны
По признаку прямоугольника (если диагонали параллелограмма равны - то он парямоугольник), делаем вывод, что ABCD - прямоугольник.
По формуле середины отрезка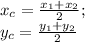
ищем координаты середины отрезков AC и BD
АС: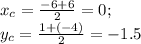
(0;-1.5)
BD: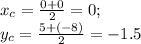
(0;-1.5)
Середины совпадают
По признаку параллелограмма (если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам - то он параллелограмм), делаем вывод, что ABCD - параллеллограмм
По формуле расстояний между двумя точками, задаными координатами
находим длины диагоналей AC и BD
Диагонали равны
По признаку прямоугольника (если диагонали параллелограмма равны - то он парямоугольник), делаем вывод, что ABCD - прямоугольник.
Доказано