Пусть — четырёхугольная пирамида, в основании которой ромб Меньшая диагональ ромба и острый угол высота пирамиды, значит, , следовательно так как — проекция на плоскость ⇒ по теореме о трёх перпендикуляров (ТТП) , следовательно, — линейный угол двугранного угла при ребре так как все двугранные углы при основании равны, то точка О — центр вписанной окружности, то есть
Найти:
Решение. Ромб состоит из четырёх равных прямоугольных треугольников:
Рассмотрим
Значит, диагональ
Рассмотрим
Высота ромба
Площадь основания пирамиды
Рассмотрим
Определим площадь треугольника
Из-за того, что у ромба все стороны равны и все двугранные углы при основании равны, то все боковые грани пирамиды будут тоже равны. Следовательно, площадь боковой поверхности
Теперь, зная площадь основания и боковой поверхности пирамиды можно найти площадь полной поверхности:
ответ: площадь полной поверхности пирамиды равна высота пирамиды равна
Объяснение:Основанием прямой призмы является равнобедренный прямоугольный треугольник. Большая боковая грань-квадрат со стороной 6 корней из 2 см.
а) найдите площадь полной поверхности этой призмы;
б) постройте сечение призмы плоскостью, проходящей через катет нижнего основания и середину противолежащего бокового ребра;
в) вычислите площадь этого сечения;
г) найдите угол между плоскостью сечения и плоскостью нижнего основания;
д) постройте линию пересечения секущей плоскости верхнего основания.
рисунок к задаче 190а) Призма прямая, т.е. её боковые ребра перпендикулярны основаниям. Боковые грани являются прямоугольниками. Площадь прямоугольника равна произведению длин смежных сторон, следовательно, площадь той грани больше, ребра которой больше. Боковые ребра параллелепипеда равны, а в основании самуую большую длину имеет гипотенуза, поэтому большая грань - ABB1A1.
И раз эта грань - квадрат, то все её стороны по 6 корней из 2, в том числе и гипотенуза основания. Пусть АС=ВС=х, из теоремы Пифагора найдем катеты основания и его площадь:
площадь основания
Теперь найдем площади боковых граней, а затем и площадь полной поверхности
Пусть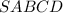 — четырёхугольная пирамида, в основании которой ромб
— четырёхугольная пирамида, в основании которой ромб 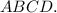 Меньшая диагональ ромба
Меньшая диагональ ромба 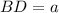 и острый угол
и острый угол 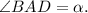
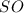 высота пирамиды, значит,
высота пирамиды, значит, 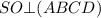 , следовательно
, следовательно 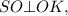 так как
так как 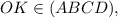
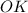 — проекция
— проекция 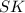 на плоскость
на плоскость 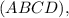
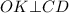 ⇒ по теореме о трёх перпендикуляров (ТТП)
⇒ по теореме о трёх перпендикуляров (ТТП) 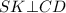 , следовательно,
, следовательно, 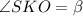 — линейный угол двугранного угла при ребре
— линейный угол двугранного угла при ребре 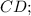 так как все двугранные углы при основании равны, то точка О — центр вписанной окружности, то есть
так как все двугранные углы при основании равны, то точка О — центр вписанной окружности, то есть 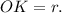
Найти: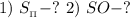
Решение. Ромб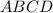 состоит из четырёх равных прямоугольных треугольников:
состоит из четырёх равных прямоугольных треугольников: 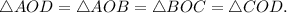
Рассмотрим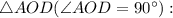
Значит, диагональ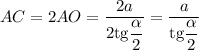
Рассмотрим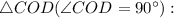
Высота ромба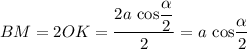
Площадь основания пирамиды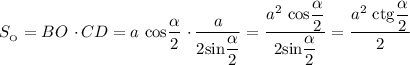
Рассмотрим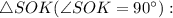
Определим площадь треугольника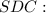
Из-за того, что у ромба все стороны равны и все двугранные углы при основании равны, то все боковые грани пирамиды будут тоже равны. Следовательно, площадь боковой поверхности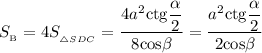
Теперь, зная площадь основания и боковой поверхности пирамиды можно найти площадь полной поверхности:
ответ: площадь полной поверхности пирамиды равна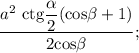 высота пирамиды равна
высота пирамиды равна 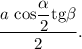
Объяснение:Основанием прямой призмы является равнобедренный прямоугольный треугольник. Большая боковая грань-квадрат со стороной 6 корней из 2 см.
а) найдите площадь полной поверхности этой призмы;
б) постройте сечение призмы плоскостью, проходящей через катет нижнего основания и середину противолежащего бокового ребра;
в) вычислите площадь этого сечения;
г) найдите угол между плоскостью сечения и плоскостью нижнего основания;
д) постройте линию пересечения секущей плоскости верхнего основания.
рисунок к задаче 190а) Призма прямая, т.е. её боковые ребра перпендикулярны основаниям. Боковые грани являются прямоугольниками. Площадь прямоугольника равна произведению длин смежных сторон, следовательно, площадь той грани больше, ребра которой больше. Боковые ребра параллелепипеда равны, а в основании самуую большую длину имеет гипотенуза, поэтому большая грань - ABB1A1.
И раз эта грань - квадрат, то все её стороны по 6 корней из 2, в том числе и гипотенуза основания. Пусть АС=ВС=х, из теоремы Пифагора найдем катеты основания и его площадь:
площадь основания
Теперь найдем площади боковых граней, а затем и площадь полной поверхности
нашли полную поверхность