c = 18+6=24 см (гипотенуза)
а =
ответ: катет равен
Верное решение уже дано. И желательно помнить данные в нем отношения проекций катетов к частям гипотенузы.
Теорема (о соотношениях в прямоугольном треугольнике).
В прямоугольном треугольнике справедливы следующие соотношения:
1) h2 = a1 · b1;
2) b2 = b1 · c;
3) a2 = a1 · c,
где b1 и a1 - проекции катетов b и a на гипотенузу с.
Но можно задачу решить несколько иначе, хотя это решение будет подлиннее.
Из подобия треугольников, образованных высотой, катетами и их проекцией на гипотенузу составить пропорцию, обозначив высоту треугольника х.
Тогда х, деленный на проекцию большего катета равен отношению проекции меньшего катета на х:
Повторю, что за х берем высоту треугольника:
х:18=6:х
Получим х²=18*6
х=√108=6√3
Теперь по теореме Пифгора больший катет найдем.
Катет = √(6√3)²+18²=12√3 см
c = 18+6=24 см (гипотенуза)
а =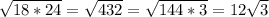
ответ: катет равен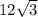
Верное решение уже дано. И желательно помнить данные в нем отношения проекций катетов к частям гипотенузы.
Теорема (о соотношениях в прямоугольном треугольнике).
В прямоугольном треугольнике справедливы следующие соотношения:
1) h2 = a1 · b1;
2) b2 = b1 · c;
3) a2 = a1 · c,
где b1 и a1 - проекции катетов b и a на гипотенузу с.
Но можно задачу решить несколько иначе, хотя это решение будет подлиннее.
Из подобия треугольников, образованных высотой, катетами и их проекцией на гипотенузу составить пропорцию, обозначив высоту треугольника х.
Тогда х, деленный на проекцию большего катета равен отношению проекции меньшего катета на х:
Повторю, что за х берем высоту треугольника:
х:18=6:х
Получим х²=18*6
х=√108=6√3
Теперь по теореме Пифгора больший катет найдем.
Катет = √(6√3)²+18²=12√3 см