Правильный четырёхугольник - это квадрат. Так как он вписан в окружность, то диаметр окружности будет равен диагонали квадрата. Диагонали квадрата пересекаются в центре и делят его на 4 одинаковых прямоугольных равнобедренных треугольника с бок. сторонами = R ⇒ S квадрата равна площади четырех треугольников:
ответ: 1
A3.
Правильный шестиугольник состоит из 6 равносторонних треугольников, стороны которых равны a, а высоты равны радиусу R. Найдем, чему равны стороны через высоту (радиус):
Площадь одного треугольника будет равна:
Площадь шестиугольника:
ответ: 2
B1.
Пусть вписанный треугольник - ΔABC, сторона = ; описанный - ΔA₁B₁C₁, сторона -
A1.
Sшестиугольника =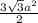
ответ: 4
A2.
Правильный четырёхугольник - это квадрат. Так как он вписан в окружность, то диаметр окружности будет равен диагонали квадрата. Диагонали квадрата пересекаются в центре и делят его на 4 одинаковых прямоугольных равнобедренных треугольника с бок. сторонами = R ⇒ S квадрата равна площади четырех треугольников:
ответ: 1
A3.
Правильный шестиугольник состоит из 6 равносторонних треугольников, стороны которых равны a, а высоты равны радиусу R. Найдем, чему равны стороны через высоту (радиус):
Площадь одного треугольника будет равна:
Площадь шестиугольника:
ответ: 2
B1.
Пусть вписанный треугольник - ΔABC, сторона =
; описанный - ΔA₁B₁C₁, сторона -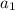 
Для ΔA₁B₁C₁ радиус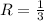
высоты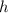 
⇒
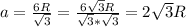
Для ΔABC радиус R =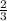
высоты 
:
⇒
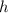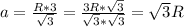
Найдем соотношение периметров и площадей:
В доказательство ненужно ответа
Объяснение:
И так，чтобы AO было равно ОВ нужно доказать, что треугольники равны.
1) угол АОС = углу ДОБ(я просто с русского пишу), так как они вертикальные (свойство вертикальных углов)
2)Треугольники равны по двум углам и стороне между ними
3) Раз треугольники равны, следовательно
напротив равных углов лежат равные стороны, следовательно
AO лежит напротив угла С равного углу Д (по условию) напротив которого лежит сторона ОВ. Отсюда АО = ОВ и следовательно точка О центр сторон.