Чтобы найти катет, не лежащий напротив угла в 30°, нужно найти сначала первый катет, равный половине гипотенузы. Т.е. катет AC, лежащий напротив угла B в 30°, равен половине гипотенузы.
Теперь найдём второй катет по теореме Пифагора .
ответ: .Задача #2.
Обозначим тр-к MOP, где PO - длина; PM - расстояние от самой постройки до основания лестницы; OM - расстояние от верхушки лестницы до её начала. Предлагаю сначала найти OM по свойству катета, лежащего напротив угла в 30°.
(метров).
Теперь найдём PM по теореме Пифагора .
(метров).
Но можно было найти катет PM по косинусу угла MPO.
ответ: (метров); (метров).Задача #3.
Пусть метров равна высота. Человек имеет рост 1,7 метров, а расстояние от фонарика до тени человека равно шагов. Т.к. тр-ки подобны, то их стороны пропорциональны. Т.е. сторона PB △PBA пропорциональна стороне MC △MCA, а также сторона AB △PBA пропорциональна стороне CA △MCA. Т.е. решим задачу пропорцией.
Чтобы найти катет, не лежащий напротив угла в 30°, нужно найти сначала первый катет, равный половине гипотенузы. Т.е. катет AC, лежащий напротив угла B в 30°, равен половине гипотенузы.
Теперь найдём второй катет по теореме Пифагора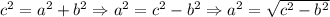 .
.
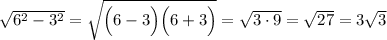
ответ:Обозначим тр-к MOP, где PO - длина; PM - расстояние от самой постройки до основания лестницы; OM - расстояние от верхушки лестницы до её начала. Предлагаю сначала найти OM по свойству катета, лежащего напротив угла в 30°.
Теперь найдём PM по теореме Пифагора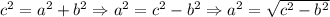 .
.
Но можно было найти катет PM по косинусу угла MPO.
ответ:Пусть метров равна высота. Человек имеет рост 1,7 метров, а расстояние от фонарика до тени человека равно
метров равна высота. Человек имеет рост 1,7 метров, а расстояние от фонарика до тени человека равно 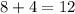 шагов. Т.к. тр-ки подобны, то их стороны пропорциональны. Т.е. сторона PB △PBA пропорциональна стороне MC △MCA, а также сторона AB △PBA пропорциональна стороне CA △MCA. Т.е. решим задачу пропорцией.
шагов. Т.к. тр-ки подобны, то их стороны пропорциональны. Т.е. сторона PB △PBA пропорциональна стороне MC △MCA, а также сторона AB △PBA пропорциональна стороне CA △MCA. Т.е. решим задачу пропорцией.
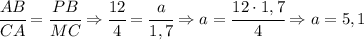 (метров).
(метров).
ответ:В треугольнике ABC ∠C = 120°, CK—биссектриса.
Доказать, что 1 / CK = 1 / AC+1 / BC. || 1 / lc = 1 / a + 1 / b ||
- - - - - - - - - - - - - - - - - - - - - - - - - - -
CK = 2*AC*BC*cos(∠ACB /2) / (AC+BC)
CK= 2*AC*BC*cos(120°/2) / (AC + BC) || cos60° =1 /2 ||
CK= AC*BC / (AC+BC) ⇔ 1 / CK = (AC+BC) / AC*BC
1 / CK = AC / AC*BC + BC / AC*BC
1 / CK = 1 / AC+ 1 / BC ч. т. д.
= = = = = = = = = = = = = = = = = = = = = = = = = = = = =
* * * P.S. ∠ACB = ∠C ; ACK =∠BCK =∠ ACB /2 = ∠C /2
CK = Lc = 2abcos(∠C/2) / (a+b) * * *
действительно :
S(ΔACB) =S(ΔACK) + S(ΔBCK) ;
(1/2)*AC*BC*sin∠C=(1/2)*AC*CK*sin(∠C/2) + (1/2)*BC*CK*sin∠C/2)
(1/2)*AC*BC*sin∠C =(1/2)*CK*sin(∠C/2) *(AC + BC)
* * * ! sin2α = 2sinα*cosα * * *
* * * sin∠C = sin(2*∠C/2) = 2sin(∠C/2)*cos(∠C/2) * * *
2AC*BC*cos(∠C/2) = CK* (AC + BC) ;
CK =2AC*BC*cos(∠C/2) / (AC+BC) || Lc=2abcos(∠C/2)/(a+b) ||