Прямая AE образует равные углы со стороной BC и медианой BM треугольника ABC. Найдите длину медианы BM, если BE=5, CE=4.

Прямая AE образует равные углы со стороной BC и медианой BM треугольника ABC. Найдите длину медианы BM, если BE=5, CE=4.

Объяснение:

Пусть О-точка пересечения АЕ и ВМ.  Углы ∠AOM=∠BOE  как вертикальные и  ∠AOM=∠BЕО по условию ⇒ ∠AOM=∠BЕО ⇒

ΔВОЕ -равнобедренный  ⇒ВЕ=ВO=5.

По т. Менелая для ΔМВС , АЕ-секущая       ,   ,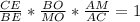

  ⇒ МО=2  ⇒ВМ=ВО+ОМ=5+2=7.

5+2 = 7

Объяснение:

Задача на теорему Фалеса.

Обозначим пересечение BM и АС как точку О. Так как углы АОМ и ВОЕ - вертикальные, они равны.

Следовательно, в треугольнике ВОЕ углы при основании равны, делаем вывод, что он равнобедренный, из чего следует, что ВЕ = ВО = 5.

Далее, собственно, для нахождения длины медианы ВМ, нам остается найти длину отрезка ОМ и прибавить её значение к 5.

Теперь, как показано на рисунке, проведем через точку М прямую, параллельную АЕ. Теперь по теореме Фалеса получается, что, так как наша новая прямая делит и параллельная ей прямая АЕ делят сторону угла С (то есть АС), на равные отрезки, то и вторую его сторону (то есть ВС), они тоже будут делить на равные отрезки, следовательно,

ЕN = CN = 4/2 = 2.

Далее, так как углы ВОЕ и ВМN, а также углы BEO и BNM попарно соответственные, все они равны. А углы МОЕ и СЕО являются смежными с равными углами, следовательно, и они равны. Таким образом у нас получается равнобедренная трапеция МОЕN, в которой боковые стороны ОМ и EN равны.

Таким образом,  ОМ = 2, а искомая сторона ВМ = 5 +2 = 7.