Прямая ka перпендикулярна плоскости ромба ABCD. Известно что угол AMO= углу CMO, угол BMO = углу DMO, где О — точка пересечения Ac. Докажите что MO перпендикуляр(ABC).
Т.к. треугольник равнобедренный, то по определению имеет 2 равные боковые стороны.
Случай 1. Пусть основание меньше боковой стороны, тогда основание = x, а боковые стороны x + 12. Периметр - это сумма всех сторон, так что составим уравнение:
x + (x+12) + (x+12) = 76
3x + 24 = 76
3x = 76 -24
3x = 52
x = 52: 3 = - основание, значит боковая сторона = x + 12 =
Случай 2. Пусть основание больше боковой стороны, тогда основание = x, а боковые стороны x - 12.
БИЛЕТ №19. 1.На листочке бумаги чертишь по линейке одну сторону. Обозначь, например конечные точки А и ВЦиркулем на линейке берешь размер второй стороны, в точку А ставишь иголочку циркуля. Карандашом циркуля проводишь дугу.Теперь берешь циркулем размер третьей стороны. Из точки В проводишь циркулем дугу. Где дуги пересеклись, поставь точку С. Это третья вершина твоего треугольника. Соедини точки А, В, С по линейке.А теперь подумай -если сумма длин сторон АС и ВС будет меньше или равна длине стороны АВ, разве твои дуги пересекутся? Попробуй для интереса. Нет, не пересекутся.Отсюда и делаем вывод ( для этого и задачу задали) -сумма двух сторон должна быть больше третьей стороны. 2.Теорема (Соотношение между сторонами и углами треугольника) . В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны АС. Докажем, что угол С больше угла В. Для этого отложим на луче АВ отрезокAD, равный стороне АС. Треугольник АСD - равнобедренный. Следовательно, Ð1 = Ð2. Угол 1 составляет часть угла С. Поэтому Ð1 < ÐC. С другой стороны, угол 2 является внешним углом треугольника ВСD. Поэтому Ð2 > ÐB. Следовательно, имеем ÐC > Ð1 = Ð2 > ÐB. Следствие: В произвольном треугольнике против большего угла лежит большая сторона. Докажем, что если в треугольнике АВС угол С больше угла В, то и сторона АВ больше стороны АС. Действительно, эти стороны не могут быть равны, так как в этом случае треугольник АВС был бы равнобедренным и, следовательно, угол С равнялся бы углу В. Сторона АВ не может быть меньше стороны АС, так как в этом случае, по доказанному, угол С был бы меньше угла В. Остается только, что сторона АВ больше стороны АС. 3.1) 2+3=5(см) - боковая сторона. 2) 5+2=7(см) - основание Проверка: 5х2=10, 10-3=7 Так же: х - основание у - боковая сторона у+2=х х+3=у2 у+2+3=у2 Так как чтобы из у получить у2 надо к у прибавить у, то (2+3)=у БИЛЕТ №201. Поставить острие циркуля в вершину угла и на обоих лучах угла отложить равные отрезки (сделать засечки). Не меняя раствора циркуля поставить поочередно острие циркуля на засечки, сделанные в шаге 1, и провести дуги, так, чтобы они пересеклись. Точку пересечения дуг соединить с вершиной угла. Это и будет биссектриса. 2.Пусть Δ ABC – равнобедренный с основанием AB , и CD – медиана, проведенная к основанию. В треугольниках CAD и CBD углы CAD и CBD равны, как углы при основании равнобедренного треугольника (по теореме 4.3), стороны AC и BC равны по определению равнобедренного треугольника, стороны AD и BD равны, потому что D – середина отрезка AB . Отсюда получаем, что Δ ACD = Δ BCD .Из равенства треугольников следует равенство соответствующих углов: ACD = BCD , ADC = BDC . Из первого равенства следует, что CD – биссектриса. Углы ADC и BDC смежные, и в силу второго равенства они прямые, поэтому CD – высота треугольника.Теорема доказана. 3.Если внешний угол А равен 120 => сам угол А = 60 (как смежные углы, т. е. 180-120). если угол А = 60 => угол В = 30 градусов. В прямоугольном треукгольнике напроитв угла в 30 градусов лежит катет равный половине гипотенузы. то есть. АВ = 2 * АС. =>2*АС + АС = 18.=> 3*АС = 18 => АС = 6 => АВ = 18 - 6 = 12БИЛЕТ №211.Возьми циркуль и выстави на нём длину чуть меньше отрезка. Иглу на начало отрезка, чертим окружность. Иглу на конец отрезка, чертим окружность. Окружности пересекутся в двух точках, соедини эти точки прямой. Прямая пересечёт середину заданного отрезка. 2.Пусть при пересечении прямых а и b секущей c сумма односторонних углов равна 180. Т. к. эти углы 3 и 4 смежные, то 3+4=180. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые параллельны. 3.AO=MH, так как ОС и ЕН - медианы треугольников ABC и MKE. Так как углы С и Е равны и ВС=КЕ, то углы АСО и МЕН также равны. Так как углы В и К равны, то соответственно углы А и М равны, из этого следует, что треугольники АСО и МЕН равны по стороне и двум прилежащим к ней углам.
Два возможных случая:
1)
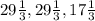
2)
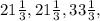
Объяснение:
Т.к. треугольник равнобедренный, то по определению имеет 2 равные боковые стороны.
Случай 1. Пусть основание меньше боковой стороны, тогда основание = x, а боковые стороны x + 12. Периметр - это сумма всех сторон, так что составим уравнение:
x + (x+12) + (x+12) = 76
3x + 24 = 76
3x = 76 -24
3x = 52
x = 52: 3 =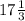
- основание, значит боковая сторона = x + 12 =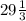 
Случай 2. Пусть основание больше боковой стороны, тогда основание = x, а боковые стороны x - 12.
Составляем уравнение
x + (x-12) + (x-12) = 76
3x - 24 = 76
3x = 76 + 24
3x = 100
x = 100:3 =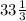
, ⇒ боковая сторона = x - 12 =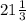 
2.Теорема (Соотношение между сторонами и углами треугольника) . В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны АС. Докажем, что угол С больше угла В. Для этого отложим на луче АВ отрезокAD, равный стороне АС. Треугольник АСD - равнобедренный. Следовательно, Ð1 = Ð2. Угол 1 составляет часть угла С. Поэтому Ð1 < ÐC. С другой стороны, угол 2 является внешним углом треугольника ВСD. Поэтому Ð2 > ÐB. Следовательно, имеем ÐC > Ð1 = Ð2 > ÐB. Следствие: В произвольном треугольнике против большего угла лежит большая сторона. Докажем, что если в треугольнике АВС угол С больше угла В, то и сторона АВ больше стороны АС. Действительно, эти стороны не могут быть равны, так как в этом случае треугольник АВС был бы равнобедренным и, следовательно, угол С равнялся бы углу В. Сторона АВ не может быть меньше стороны АС, так как в этом случае, по доказанному, угол С был бы меньше угла В. Остается только, что сторона АВ больше стороны АС.
3.1) 2+3=5(см) - боковая сторона. 2) 5+2=7(см) - основание Проверка: 5х2=10, 10-3=7 Так же: х - основание у - боковая сторона у+2=х х+3=у2 у+2+3=у2 Так как чтобы из у получить у2 надо к у прибавить у, то (2+3)=у БИЛЕТ №201. Поставить острие циркуля в вершину угла и на обоих лучах угла отложить равные отрезки (сделать засечки). Не меняя раствора циркуля поставить поочередно острие циркуля на засечки, сделанные в шаге 1, и провести дуги, так, чтобы они пересеклись. Точку пересечения дуг соединить с вершиной угла. Это и будет биссектриса.
2.Пусть Δ ABC – равнобедренный с основанием AB , и CD – медиана, проведенная к основанию. В треугольниках CAD и CBD углы CAD и CBD равны, как углы при основании равнобедренного треугольника (по теореме 4.3), стороны AC и BC равны по определению равнобедренного треугольника, стороны AD и BD равны, потому что D – середина отрезка AB . Отсюда получаем, что Δ ACD = Δ BCD .Из равенства треугольников следует равенство соответствующих углов: ACD = BCD , ADC = BDC . Из первого равенства следует, что CD – биссектриса. Углы ADC и BDC смежные, и в силу второго равенства они прямые, поэтому CD – высота треугольника.Теорема доказана.
3.Если внешний угол А равен 120 => сам угол А = 60 (как смежные углы, т. е. 180-120). если угол А = 60 => угол В = 30 градусов. В прямоугольном треукгольнике напроитв угла в 30 градусов лежит катет равный половине гипотенузы. то есть. АВ = 2 * АС. =>2*АС + АС = 18.=> 3*АС = 18 => АС = 6 => АВ = 18 - 6 = 12БИЛЕТ №211.Возьми циркуль и выстави на нём длину чуть меньше отрезка. Иглу на начало отрезка, чертим окружность. Иглу на конец отрезка, чертим окружность. Окружности пересекутся в двух точках, соедини эти точки прямой. Прямая пересечёт середину заданного отрезка.
2.Пусть при пересечении прямых а и b секущей c сумма односторонних углов равна 180. Т. к. эти углы 3 и 4 смежные, то 3+4=180. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые параллельны.
3.AO=MH, так как ОС и ЕН - медианы треугольников ABC и MKE. Так как углы С и Е равны и ВС=КЕ, то углы АСО и МЕН также равны. Так как углы В и К равны, то соответственно углы А и М равны, из этого следует, что треугольники АСО и МЕН равны по стороне и двум прилежащим к ней углам.