Прямоугольный треугольник вращается вокруг своего меньшего катета. определи площадь боковой поверхности конуса, который образовался. длины катетов треугольника 8 и 15 см. ответ: sбок.= πсм2
Рассмотрим первый рисунок, нужно найти сторону BC, если известны стороны AB и AC, а также треугольник ABC прямоугольный. Значит мы можем воспользоваться теоремой Пифагора: AB^2 = AC^2 +BC^2
Тогда, получаем 169 = 25+BC^2, тогда BC^2 = 169-25=144, BC = корень из 144 = 12
На втором рисунке нужно найти также BC. Запишем несколько теорем Пифагора: AB^2=BH^2+AH^2, BC^2 = BH^2+HC^2
225 = 16x^2+9x^2, откуда 225 = 25x^2, x^2 = 9, значит x = 3 (т.к. стороны не могут иметь отрицательную длину), и тогда AC = 4x = 4*3 = 12, BC = 3x = 3*3 = 9
Рассмотрим первый рисунок, нужно найти сторону BC, если известны стороны AB и AC, а также треугольник ABC прямоугольный. Значит мы можем воспользоваться теоремой Пифагора: AB^2 = AC^2 +BC^2
Тогда, получаем 169 = 25+BC^2, тогда BC^2 = 169-25=144, BC = корень из 144 = 12
На втором рисунке нужно найти также BC. Запишем несколько теорем Пифагора: AB^2=BH^2+AH^2, BC^2 = BH^2+HC^2
Подставляем числа: 169x^2 = 24^2+AH^2, BC^2= 24^2+HC^2
Сложим уравнения, получим BC^2+169x^2 = 2*24^2 +AC^2 = 1152+100x^2
Тогда получаем BC^2 = 1152-69x^2 (так как икс не дан - нельзя найти BC)
Рисунок третий, теорема Пифагора: AB^2 = AC^2+BC^2
225 = 16x^2+9x^2, откуда 225 = 25x^2, x^2 = 9, значит x = 3 (т.к. стороны не могут иметь отрицательную длину), и тогда AC = 4x = 4*3 = 12, BC = 3x = 3*3 = 9
Осевое сечение цилиндра - квадрат площадью S=a² .
a) S=16 cм² . Тогда сторона квадрата равна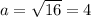 см .
см .
Высота цилиндра равна Н=а=4 см .
Радиус основания равен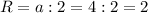 см .
см .
Площадь полной поверхности цилиндра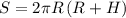 .
.
б) S=121 cм² . Тогда сторона квадрата равна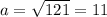 см .
см .
Высота цилиндра равна Н=а=11 см .
Радиус основания равен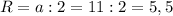 см .
см .
Площадь полной поверхности цилиндра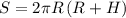 .
.
в) S=441 cм² . Тогда сторона квадрата равна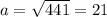 см .
см .
Высота цилиндра равна Н=а=21 см .
Радиус основания равен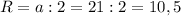 см .
см .
Площадь полной поверхности цилиндра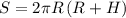 .
.