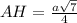Пусть d - расстояние от центра окружности с радиусом Rдо прямой l . Каково взаимное расположение прямой l и окружности. Если: 1) R=8cm,d=6cm; 2) R=10cm,d=8,4 cm; 3) R=14,4dm,d=7,4dm; 4) R=1,6dm,d=24cm; 5) R=4cm,d=40mm
1) Уравнение 3х-4у+24=0 преобразуем в уравнение вида у = кх + в. В уравнениях такого вида коэффициент к показывает крутизну (точнее тангенс угла) наклона графика функции к оси х (абсцисс), а величина в дает точку пересечения этим графиком оси у (ординат). 3х-4у+24=0 4у = 3х +24 у = (3/4)х + 6. Уравнение х^2+у^2=25 - зто уравнение окружности в центре координат с радиусом, равным √25 = 5. Для нахождения взаимного расположение прямой и окружности надо решить систему уравнений: 3х-4у+24=0 и х^2+у^2=25. Совместное решение дает результат: х₁ = -4; у₁ = 3; х₂ = -44/25; у₂ = -117/25, то есть прямая пересекает окружность в двух точках. 2) Аналогично решается второе задание - в этом случае графики заданных уравнений не песекаются.
Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.
A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
В уравнениях такого вида коэффициент к показывает крутизну (точнее тангенс угла) наклона графика функции к оси х (абсцисс), а величина в дает точку пересечения этим графиком оси у (ординат).
3х-4у+24=0
4у = 3х +24
у = (3/4)х + 6.
Уравнение х^2+у^2=25 - зто уравнение окружности в центре координат с радиусом, равным √25 = 5.
Для нахождения взаимного расположение прямой и окружности надо решить систему уравнений: 3х-4у+24=0 и х^2+у^2=25.
Совместное решение дает результат:
х₁ = -4; у₁ = 3;
х₂ = -44/25; у₂ = -117/25, то есть прямая пересекает окружность в двух точках.
2) Аналогично решается второе задание - в этом случае графики заданных уравнений не песекаются.
Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.
A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
-----------
теперь по теореме пифагора найдем AH:
ответ: