1) Наверное, все-таки, РАВНЫЕ отрезки, а не РАЗНЫЕ ?..)) По теореме Фалеса параллельные прямые откладывают на сторонах угла пропорциональные отрезки. Так как оба отрезка равны, то прямая, проведенная через концы этого отрезка будет параллельна основанию треугольника и, следовательно, будет перпендикулярна медиане к основанию. Последнее следует из того, что в равнобедренном треугольнике медиана к основанию является также биссектрисой угла при вершине и высотой данного треугольника. Так как данный отрезок перпендикулярен медиане и делится ей пополам так же, как и основание, можно утверждать, что расстояния от концов отрезка до любой точки на медиане будут равны между собой.
2) Так как CED - равнобедренный, то ∠ECD = ∠EDC => ∠ECM = ∠MCD = ∠EDH = ∠HDC Тогда ΔHDC = ΔMCD по стороне и двум углам: (CD - общая, ∠HDC = ∠MCD, ∠HCD = ∠MDC) Отсюда следует, что HC = MD.
В ΔСАН и ΔMAD: HC = MD, ∠HCM = ∠MDA, ∠MAD = ∠HAC => эти треугольники равны по стороне и двум углам
5. 28
6. 21
Объяснение:
5. АВ = 42, 2BC = AC - это если наше условие написать на математическом языке. Чтобы решить эту задачу, нужно составить уравнение
AC + BC = 42
Но чтобы у нас не было двух неизвестных, нужно один отрезок выразить через другой. Для этого мы и переписали условие
АС + BC = 2BC + BC
2BC + BC = 42
3BC = 42
BC = 42 : 3 = 14
Если BC = 14, то АС = 42 - 14 = 28.
6. АВ = 49, АС =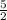
CB или 2,5СВ
Чтобы найти АС, мы переписали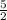
в 2,5 , чтобы проще было посчитать. АС - это две части и одна половинка этой части СВ. То есть,
СВ + СВ +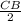
= AC.
СВ + СВ +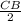
+ СВ = 49
3СВ +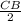
= 49, чтобы легко избавиться от некрасивой дроби, нужно две части уравнения домножить на 2
6СВ + СВ = 98
7СВ = 98
СВ = 14, следовательно АС = 49 - 14 = 35
Раз нам надо найти АС - СВ, то 35 - 14 = 21.
По теореме Фалеса параллельные прямые откладывают на сторонах угла пропорциональные отрезки. Так как оба отрезка равны, то прямая, проведенная через концы этого отрезка будет параллельна основанию треугольника и, следовательно, будет перпендикулярна медиане к основанию. Последнее следует из того, что в равнобедренном треугольнике медиана к основанию является также биссектрисой угла при вершине и высотой данного треугольника.
Так как данный отрезок перпендикулярен медиане и делится ей пополам так же, как и основание, можно утверждать, что расстояния от концов отрезка до любой точки на медиане будут равны между собой.
2) Так как CED - равнобедренный, то ∠ECD = ∠EDC =>
∠ECM = ∠MCD = ∠EDH = ∠HDC
Тогда ΔHDC = ΔMCD по стороне и двум углам:
(CD - общая, ∠HDC = ∠MCD, ∠HCD = ∠MDC)
Отсюда следует, что HC = MD.
В ΔСАН и ΔMAD: HC = MD, ∠HCM = ∠MDA, ∠MAD = ∠HAC =>
эти треугольники равны по стороне и двум углам