1)Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм. Пусть в четырехугольнике абсд стороны аб и сд параллельны и аб=сд проведем диагональ ас, делящую данный четырехугольник на два треуг-а: абс и сда. Эти треуг-и равны по двум сторонам и углу между ними, поэтому уголСАД=уголБСА, но эти углы накрест лежащии при пересечении прямых АД и БС секущей АС, следовательно, ад//бс Таким образом, в четырехугольнике АБСД противоположные стороны попарно параллельны, а значит АБСД- параллелограмм 2) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм. Проведем диаг АС данного четырехугольника АБСД, делящую его на треуг-и АБС и СДА. Эти треуг-и равны по трем сторонам, поэтому угл БАС равен углу САД=> аб//сд. Так как аб=сд и аб//сд, то абсд - параллелограмм.
Даны векторы k(-1;2), s(5;-12), c(2;x). Найдите: a)cos(∠k, s) ; b) число x, если k и c - коллинеарные; c) число x, если s и c - перпендикулярны.
Объяснение:
a)Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение их длин.
Найдем длины векторов:
Длина вектора |k|=√( (-1)²+2²)=√(1 +4)=√5,
Длина вектора |s|=√( 5²+(-12)²)=√(25+144)=√169=13,
Скалярное произведение k*s=-1*5+2*(-12)=-5-24=-29
cos(∠k, s)= .
b) Два вектора коллинеарные ,если их координаты пропорциональны, значит для k(-1;2),c(2;x) :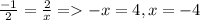 ;
;
c)Вектора перпендикулярны , если их скалярное произведение равно нулю : ⇒ 12x=10 , x=
⇒ 12x=10 , x= .
.