В задании, очевидно, надо понимать фразу так: расстояние от СТОРОНЫ основания до противолежащей боковой грани равно 5 корень из 3.
Проведём осевое сечение пирамиды перпендикулярно стороне основания. Получим равнобедренный треугольник, углы α при основании которого равны двугранным углам пирамиды, а высота Н равна высоте пирамиды.
Основание этого треугольника равно стороне основания пирамиды.
Находим синус угла при основании треугольника:
sin α = 5√3/10 = √3/2. Значит, α = 60°.
Отсюда находим высоту пирамиды Н = 5*tg 60° = 5√3.
Получаем ответ: V = (1/3)SoH = (1/3)*10²*5√3 = 500√3/3 куб.ед.
Р(0; -44)
Объяснение:
1) Представим координаты точки K как (х₁; у₁), точки М как (х₂; у₂), точки P как (х₃; у₃)
Найдём разницу соответствующих координат точек М и К:
Δх = (х₂ - х₁) = 4-6 = -2
Δу = (у₂ - у₁) = -8 - 10 = -18
Эти величины показывают нам как изменяется координата точки на отрезке, в зависимости от удаления т.М от т. K.
Так как известно, что т. М делит отрезок РК в отношении 2:1, начиная от т. Р, то коэффициент соотношения длин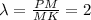 .
.
Тогда и изменение (дельта) координат от т.М до т.Р будет больше в 2 раза. Значит для вычисления координат т. Р можно записать выражения:
В задании, очевидно, надо понимать фразу так: расстояние от СТОРОНЫ основания до противолежащей боковой грани равно 5 корень из 3.
Проведём осевое сечение пирамиды перпендикулярно стороне основания. Получим равнобедренный треугольник, углы α при основании которого равны двугранным углам пирамиды, а высота Н равна высоте пирамиды.
Основание этого треугольника равно стороне основания пирамиды.
Находим синус угла при основании треугольника:
sin α = 5√3/10 = √3/2. Значит, α = 60°.
Отсюда находим высоту пирамиды Н = 5*tg 60° = 5√3.
Получаем ответ: V = (1/3)SoH = (1/3)*10²*5√3 = 500√3/3 куб.ед.