1. В тексте исправил вопрос на "найти длину проекции наклонной", а то получается , что искать нужно известную величину. Угол между наклонной и плоскостью - это угол между наклонной и ее проекцией на плоскость. Имеем прямоугольный треугольник: гипотенуза 8 см, один угол 60°. ВТОРОЙ ОСТРЫЙ 30°. Катет, лежащий против него равен половине гипотенузы, 8/2 = 4 см.Это проекция наклонной. Расстояние (это длина перпендикуляра) равно 4 * sin 60° = 2√3 см. 2. строим линейный угол двугранного угла и ставим размеры. Получаем прямоугольный треугольник с катетом 4 м и гипотенузой 8 м. Значит, угол равен 30°.
Угол между наклонной и плоскостью - это угол между наклонной и ее проекцией на плоскость. Имеем прямоугольный треугольник: гипотенуза 8 см, один угол 60°. ВТОРОЙ ОСТРЫЙ 30°. Катет, лежащий против него равен половине гипотенузы, 8/2 = 4 см.Это проекция наклонной. Расстояние (это длина перпендикуляра) равно 4 * sin 60° = 2√3 см.
2. строим линейный угол двугранного угла и ставим размеры. Получаем прямоугольный треугольник с катетом 4 м и гипотенузой 8 м. Значит, угол равен 30°.
1.
∆АВС≈∆AMK по 3-ём углам (∠А-общий, ∠AMK=∠ABC как соответственные при секущей AB и MK║BC, ∠AKM=∠ACB как соответственные при секущей AC и MK║BC) ⇒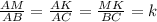
AM/AB=4/6=MK/BC=8/x x=6·8:4=12 см - BC
AM/AB=4/6=AK/AC=9/y y=6·9:4=13,5 см - AC
ответ: 12 см - BC и 13,5 см - AC
2.
По свойству медиан в треугольнике:
BO=8=2x ⇒ OK=x=4 см
AD=3х=24 ⇒ OD=x=8 см, а AO=2x=16 см
ответ: ОК=4; АО=16; ОD=8
3.
ВD - биссектриса ∆АВС ⇒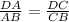
Пусть DA=x, тогда DC = 11-x
Составим пропорцию: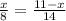
14x=88-8x
14x+8x=88
22x=88
x=4 см - сторона AD
11-4=7 cм- сторона DC
ответ: 4 см - сторона AD и 7 cм- сторона DC