Ранов • РУКАВИЧКИ
Снеговик у Снеговички
Взял на время рукавички.
День второй идёт.
он их всё не отдаёт!
Говорит, что в рукавичках
согреваются синички.
Вот когда зима пройдёт,
рукавички он вернёт.
Спиши первое предложение стихотворения. Найди
В нём главные слова. Назови в них мягкие согласные
Звуки.
• Выпиши из предложения слова парами, поставь
от слова к слову вопрос (смотри упр. 74, с. 62).

Показать ответ

Ответ:

ТыУмНыЙ

15.10.2020 13:12

∠С=30°,∠А=90°,∠В=60°

Объяснение:

Дано: AD⊥BC, ВО=ОС. ∠ВАD=∠DАО=∠ОАС

Найти: ∠А,∠В,∠С ΔАВС

Пусть ∠ВАD=∠DАО=∠ОАС=х

1) Рассмотрим ΔВАО. АD - высота. ∠ВАD=∠DАО ⇒ АD - биссектриса.

Если в треугольнике медиана совпадает с биссектрисой, то треугольник равнобедренный. ⇒ΔВАО - равнобедренный. В равнобедренном треугольнике высота является также медианой. ⇒

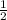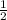ВD=DО= $\frac{1}{2}$ ВО= $\frac{1}{2}$ ОС.

2) Дополнительное построение: Проведём ОМ⊥АС.

Рассмотрим прямоугольные треугольники АDО и АМО.

∠DАО=∠ОАС - по условию, АО - общая.

Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.

⇒ΔАDО = ΔАМО

Из равенства треугольников следует равенство катетов:

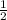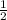DО = МО = $\frac{1}{2}$ ВО= $\frac{1}{2}$ ОС.

3) Рассмотрим прямоугольный треугольник ОМС (∠М=90°).

Из доказанного выше МО=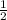 $\frac{1}{2}$ ОС. Т.е. катет МО равен половине гипотенузы ОС.

Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30°.

Следовательно ∠С=30°

4) Рассмотрим прямоугольный треугольник АDC(∠D=90°).

По свойству острых углов прямоугольного треугольника

∠DАС=90°-∠С=90°-30°=60°.

По условию ∠DАС=2х ⇒ 2х=60°, х=30°

5) ∠ВАС=3х=3*30°=90°

∠А треугольника АВС = 90°

Так как сумма углов треугольника равна 180°, то ∠В треугольника АВС будет равен: ∠В=180°-∠А-∠С=180°-90°-30°=60°

Висота і медіана, проведені з однієї вершини трикутника,розділили його кут на три рівні частини. Зна

0,0(0 оценок)

Ответ:

01lina10

26.09.2021 00:43

Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон трапеции и проходящий параллельно ее основаниям.

Пусть в трапеции АВСD средняя линия EF пересекает диагонали трапеции АС и ВD в точках М и N соответственно. Тогда в треугольнике АВС отрезок ЕМ является средней линией, поскольку ЕМ║ВС как часть средней линии трапеции и точка Е - середина стороны АВ.

Следовательно, Сторона АС треугольника точкой М делится пополам.

Аналогично в треугольнике ВCD отрезок NF - средняя линия и делит сторону BD пополам.

Таким образом, доказано, что средняя линия трапеции делит ее диагонали пополам, то есть проходит через их середины, что и требовалось доказать.