Рассчитай количество железа, необходимого для полого шара с толщиной стенки 3 мм и внешним радиусом 9 см.

* * * * * * * * * * * * * * * * * * * * * * * * * *

В равнобедренной трапеции диагональ является биссектрисой. Найдите площадь трапеции, если боковая сторона - 25 см, основание 39 см

ответ:    768 см².

Объяснение:  Пусть   ABCD  равнобедренная трапеция

AD и BC основания трапеции  ( AD  ||  BC  )   AD =39  см ,

ВA = CD =25 см  и   ∠ BAC = ∠ DAC .  

S(ABCD) = h*(AD+BC)/2   -?

∠ BCA= ∠ DAC как накрест лежащие углы  ( BC || AD , CA секущая) ,

следовательно  ∠ BCA= ∠ DAC =∠ BAC , т.е.  ΔBAC  равнобедренный

BA = BC =25 см     получили   BA  = CD =25 см .

Проведем  BB₁ ⊥ AD  и  CC₁ ⊥ AD .  BCC₁B₁ _прямоугольник  BB₁ =CC₁

B₁C₁ = BC =25 см  ;  Δ BB₁A = Δ CC₁D(гипотен. BA= CD  и катеты BB₁ =CC₁).

AB₁ =(AD - BC)/2 =(39 - 25)/2 см=7 см .

Из  Δ BB₁A по теореме Пифагора:

BB₁ =√(BA²  -AB₁² ) =√(25²  -7)² =√(625  -49) =√576=24 (см) .

* * * h=√(25²-7)² =√(25 -7)(25 +7) =√(18*32) √(9*2*16*2)=3*2*4=24 * * *

S(ABCD) = h*(AD+BC)/2 =24(39+25)/2 =24*32 = 768 (см²).

Объяснение:

a) Модуль АМ=5.3 cм

б) (АВ-АС)*ВС= {0; 0; 0}

в) ∠ВДА=60°

г) векторы не колинеарны

Объяснение:

a) М(-0,5;1;2) СЕРЕДИНА ОТРЕЗКА ВС

АМ(-4,5;2;2)

Модуль АМ=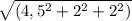=5.3 cм

б) АВ-АС=(-6;1;2)-(-3;3;2)=(-3;-2;0)

(АВ-АС)*ВС=(-3;-2;0)*(3;2;0)= {0; 0; 0}

i j k

ax ay az

bx by bz

 =  

i j k

-3 -2 0

3 2 0

 = i ((-2)·0 - 0·2) - j ((-3)·0 - 0·3) + k ((-3)·2 - (-2)·3) =  

 = i (0 - 0) - j (0 - 0) + k (-6 + 6) = {0; 0; 0}

в) Из ΔВДА найдем ∠ВДА по теореме косинуса, сторона лежащая напротив этого угла АВ

АВ^2=BD^2+AD^2-2BD*ADcos∠ВДА

Модуль АВ(-6;1;2)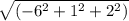 =6,4 cм

Модуль ВС(3;2;0)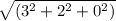 =3,6 cм

Модуль АД(-1;2;7)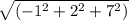 =7,35 cм

6.4^2=3.6^2+7,35^2-2*3.6*7,35cos∠ВДА

cos∠ВДА=0,5; ∠ВДА=60°

г) Два вектора a и b коллинеарны, если существует число n такое, что

a = n · b

Векторы АВ(-6;1;2) АС(-3;3;2)  АД (-1;2;7) имеют общее начало т А

Отношение координат разное (2; 1/3; 1) Поэтому векторы не колинеарны