Возьмём теорему Фалеса, как основу для решения данной задачи (ибо только она подходит для решения)
Надеюсь, что я правильно понял, что прямая MN параллельно прямой NP.
Составил рисунок, наиболее подходящий для этой задачи (по другому тоже есть альтернативный вариант, но он рассматривается в 11-ых класса в разделе Физика)
Из следствия теоремы Фалеса, из курса 8 класса мы вспоминаем, что параллельные прямые отсекают на сторонах угла пропорциональные отрезки, то есть KO : MK = PO : NP из этого выражаем =>
Возьмём теорему Фалеса, как основу для решения данной задачи (ибо только она подходит для решения)
Надеюсь, что я правильно понял, что прямая MN параллельно прямой NP.
Составил рисунок, наиболее подходящий для этой задачи (по другому тоже есть альтернативный вариант, но он рассматривается в 11-ых класса в разделе Физика)
Из следствия теоремы Фалеса, из курса 8 класса мы вспоминаем, что параллельные прямые отсекают на сторонах угла пропорциональные отрезки, то есть KO : MK = PO : NP из этого выражаем =>
=> KO = MK ·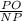
- подставляем => KO = 15 · 
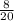= 6
ответ: KO = 6 см.
Дано :
ΔАВС.
D ∈ AB.
E ∈ BC.
DE ║ AC.
DB = 2,8 см.
АВ = 14 см.
АС = 13 см.
Найти :
ED = ?
Краткое -
∢BDE = ∢BАC, т. к. соответственные углы.
∢BЕD = ∢BCA, т. к. соответственные углы ⇒ ΔABС ∼ ΔDBЕ.
DE = 2,6 см.
Полное -
∠В - общий для ΔАВС и ΔDBЕ.
Рассмотрим соответственные ∠BED и ∠ВСА при пересечении параллельных прямых ED и АС секущей ЕС.
При пересечении двух параллельных прямых секущей соответственные углы равны.Тогда -
∠BED = ∠ВСА.
Следовательно, ΔАВС ~ ΔDBЕ по двум равным углам (первый признак подобия треугольников).
В подобных треугольниках против равных углов лежат сходственные стороны.Тогда пара сторон -
АВ и BD - сходственные стороны
АС и DE - сходственные стороны.
Отношения сходственных сторон подобных треугольников равны.То есть -
ED = 2,6 см.
2,6 см.