Расстояние от точки пересечения диагоналей прямоугольника до его смежных сторон равно 5,9 см и 5,7 см. Начерти рисунок и вычисли периметр прямоугольника.

ответ: P=
см.

ответ:ответ:

а) угол А= углу М

б) АВ=МК

Объяснение:Даны равнобедренные треугольники АВС и МКО с основаниями ВС и КО, АВ=МК. Какое условие достаточно добавить, чтобы данные треугольники были равны:

а) по первому признаку равенства треугольников;

б) по третьему признаку равенства треугольников?

а) угол А= углу М

б) ВС=КО

Есть ошибка?

Даны равнобедренные треугольники АВС и МКО с основаниями ВС и КО, ВС=КО. Какое условие достаточно добавить, чтобы данные треугольники были равны:

а) по второму признаку равенства треугольников;

б) по третьему признаку равенства треугольников?

а) угол А= углу М

б) АВ=МК

Объяснение:

Задание №1.

Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.

Задание №2.

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то этот треугольник - прямоугольный.

Задание №3.

Рассмотрим четыре равных прямоугольных треугольника.

Соединим эти четыре прямоугольных треугольника.

Получим квадрат, в который вписан еще один квадрат, похожий на ромб.

Одна половина стороны квадрата равна a, другая - b. Площадь первого квадрата будет равна (a+b)^2.

Сторона второго квадрата равна с, следовательно, площадь будет равна c^2.

А площадь всего многоугольника будет равна сумме площадей треугольников и второго квадрата.

Запишем это так:

4 * 0,5 * a * b + c^2 = a^2 + 2ab + b^2

Слева получим:

2ab + c^2 = a^2 + 2ab + b^2

2ab можем уничтожить.

Останется c^2 = a^2 + b^2

Теорема доказана.

А вот что такое "Приведите пример Пифагором треугольника" я не знаю.

4. Формула Герона для нахождения площади произвольного треугольника:

S =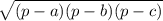

Где p - полупериметр треугольника, а все остальное - его стороны.