Равнобедренные треугольники ABC и ADC имеют общее основание. Точки Ви D лежат в разных по-
Дуплоскостях относительно прямой Ас. Докажи-
те, что:
1) лучи BD и DB являются биссектрисами углов.
ABC и ADC; ;
2) BDIAC.
- Дано: |_
BAD = 46°, |_ADC = 105°.
Вычислите градусные меры углов:
1) CAD,
2) BDM.
B
46
D
M
A
105
с​

Вариант 1

№1.  Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.

Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора:  BC = = = =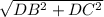

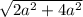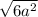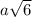
№2. Пусть D - данная точка. DB и DC - наклонные. Проведем AD — перпендикуляр к плоскости α. Тогда АВ и АС — проекции наклонных на плоскость α. Тогда ΔABD и ΔACD — прямоугольные, равнобедренные. Так что АВ = АC = AD = а.

DC = DB = a : sin45 =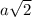

Так что ΔBDC — равнобедренный, а поскольку ∠BDC = 60°, то значит треугольник BDC — равносторонний, т.е.

DB = DC = BC =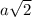

(Дальше долко)

поскольку это равнобедренный треугольник то его две стороны должны быть одинаковой длины

тоесть или 5 см и 5 см или 2 см и 2 см

рассмотрим эти два случая (фото)

за признаком треугольника :

Длина третьей стороны треугольника должна быть больше суммы двух других сторон, и не может быть и меньше разности двух других сторон

рассмотрим случай где две стороны 5 и одна 2

5-5<2<5+5

0 <2<10

....

5-2<5<5+2

3<5<7

неравенство верное,значит такой треугольник существует

--------------------------------

рассмотрим случай где две стороны 2 и одна 5

2-2<5<2+2

0<5<4

поскольку 5>4 то такого треугольника не существует

ОТВЕТ: ДВЕ СТОРОНЫ ТРЕУГОЛЬНИКА РАВНЫ 5 СМ И ТРЕТЬЯ 2 СМ