Равнобедренный треугольник ABC с основанием AC вписан в окружность с центром в точке O, причем точка O находится во внутренней области этого треугольника. Найдите ∠ABC, если ∠AOB=133 ∘. ответ дайте в градусах.
Прежде чем рассматривать 6 угольник. Давайте рассмотрим 4 угольник. Чуть позже объясню почему. (рисунок 1) Соединим середины сторон 4 угольника ABCD. Проведем диагональ AC Очевидно что MN-средняя линия треугольника ABC,откуда MN||AC, также PQ-cредняя линия треугольника ACD ,то PQ||AC. То выходит что MN||PQ. Анологично при проведении другой диагонали докажем что MQ||NP. То MNPQ-параллелограмм. Рассмотрим наконец 6 угольник проведем в нем диагональ D (2 рисунок) Она бьет его на 2 четырехугольника. На ней отметим точку S,являющуюся серединой диагонали. То из выше сказанного A1A2A3S-параллелограмм. Понятно , что для точек A1 A2 A3 cуществует одна и только одна точка H, для которой A1A2A3H-параллелограмм. А значит точка H совпадает с точкой S. H=S Тк второй такой точки не существует. Рассуждая анологично для второго 4 угольника. Покажем что M=S. А значит формально говоря: H=M ЧТД.
Чуть позже объясню почему. (рисунок 1)
Соединим середины сторон 4 угольника ABCD.
Проведем диагональ AC
Очевидно что MN-средняя линия треугольника ABC,откуда
MN||AC, также PQ-cредняя линия треугольника ACD ,то PQ||AC.
То выходит что MN||PQ. Анологично при проведении другой диагонали докажем что MQ||NP. То MNPQ-параллелограмм.
Рассмотрим наконец 6 угольник проведем в нем диагональ D (2 рисунок)
Она бьет его на 2 четырехугольника.
На ней отметим точку S,являющуюся серединой диагонали.
То из выше сказанного A1A2A3S-параллелограмм.
Понятно , что для точек A1 A2 A3 cуществует одна и только одна точка
H, для которой A1A2A3H-параллелограмм. А значит точка H совпадает с точкой S. H=S Тк второй такой точки не существует.
Рассуждая анологично для второго 4 угольника. Покажем что
M=S.
А значит формально говоря: H=M
ЧТД.
3) Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Так как углы, взятые в порядке следования относятся как 1:3:4 , то ∠А=х , ∠В=3х , ∠С=4х и ∠А+∠С=х+4х=5х=180° , х=36° .
∠А=36° , ∠В=3*36°=108° , ∠С=4*36°=144°
Сумма внутренних углов четырёхугольника равна 360°.
∠D=360°-36°-108°-144°=72°
Или ∠В+∠D=5х , ∠D=5x-∠B=3x-3x=2x , 2x=2*36°=72° .
4) Сторона правильного треугольника равна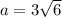 .
.
Радиус вписанной окружности в прав. тр-к равна 1/3 его высоты, то есть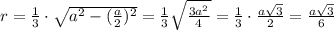 .
.
Сторона прав.четырёхугольника - квадрата, описанного около окружности, равна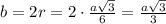 .
.
Периметр квадрата равен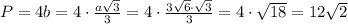 см.
см.