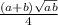Равнобокая трапеция с основаниями a и b описана - вопрос №3860245 от ttttrrrrtttr 22.03.2020 01:20

Question

Геометрия: Равнобокая трапеция с основаниями a и b описана около окружности. через конец верхнего основания и центр окружности o проведена прямая, отрезающая от трапеции треугольник. найти его площадь.

ttttrrrrtttr · Answer

Пусть СО пересекает AD в точке Е1 , СО -биссектриса угла С => угол ВСЕ1 = УГЛУ Е1СD , но угол ВСЕ1 = углу СЕ1D ( как накрест лежащие ) => угол СЕ1D = углу Е1СD => треугольник СЕ1D - равнобедренный => E1D = CD = (a+b)/2 = > точки Е и Е1 совпадают (доп. объяснение к задаче)

ответ: $\frac{(a+b)\sqrt{ab} }{4}$

Равнобокая трапеция с основаниями a и b описана около окружности. через конец верхнего основания и ц