Прежде всего замечаем, что радиус описанной окружности равен 2/3 высоты равностороннего треугольника. В свою очередь высота равностороннего треугольника:
h = a√3 / 2, где a - сторона треугольника, то есть
R = 2/3 · a√3 / 2 = a√3 / 3 ⇒ a = R√3 ⇒ a = 18√3 см
Примечание:
Так как задача на применение формулы - можно обойтись без чертежа.
R= (корень из 3 разделить на 3) а
а= 18 / (корень из 3 разделить на 3)
а= 54 / корень из 3
Прежде всего замечаем, что радиус описанной окружности равен 2/3 высоты равностороннего треугольника. В свою очередь высота равностороннего треугольника:
h = a√3 / 2, где a - сторона треугольника, то есть
R = 2/3 · a√3 / 2 = a√3 / 3 ⇒ a = R√3 ⇒ a = 18√3 см
Примечание:
Так как задача на применение формулы - можно обойтись без чертежа.
18·√3 см
Объяснение:
По условию равносторонний треугольник ABC вписан в окружность, то в свою очередь окружность является описанной около треугольника ABC (см. рисунок).
Как известно, радиус R описанной окружности и сторона a равностороннего треугольника связаны формулой:
Отсюда: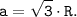
Так как радиус окружности известен R = 18 см, то можем найти сторону треугольника:
a = 18·√3 см.