РЕШИТЬ 1. Вычислите скалярное произведение векторов m ⃗ и n ⃗, если |m ⃗ | = 8, |n ⃗ | = 5, а угол между ними равен 60°.
2. Вычислите скалярное произведение векторов a ⃗ и b ⃗, если a ⃗ {8; -3}, b ⃗ {9; 14}.

3. Вычислите косинус угла между векторами a ⃗ и b ⃗, если a ⃗ {9;-12 }, b ⃗ {-4; 3}.

4. Даны векторы m ⃗ {8; 5} и n ⃗ {y; –16}. При каком значении у эти векторы перпендикулярны?

5. Найдите угол между ненулевыми векторами c ⃗ {х; у} и d ⃗ {y; -х}

Показать ответ

Ответ:

совуша2007

29.12.2021 17:00

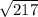
а) $\sqrt{217}$

б)-28

Объяснение:

Чтобы найти координаты вектора XY для точек X(x1,x2,x3) и Y(y1,y2,y3) нужно переместить X в 0, т.е просто отнять x1 из y1 и т.д. Итого XY(y1-x1, y2-x2, y3-x3). Аналогично вычисляем:

AB(1-2,-2-4,3-5)=AB(-1,-6,-2)

BC(-1-1,-2-(-2),4-3)=BC(-2,0,1)

AC(-1-2,-2-4,4-5)=AC(-3,-6,1)

Вектор XY*k получается домножением каждой координаты на k, чтобы вычесть вектора нужно из координат первого вектора вычесть координаты второго вектора:

a=3AB-4AC=(3*(-1)-4*(-3),3*(-6)-4*(-6),3*(-2)-4*1)=(9,6,-10)

Длина вектора a - среднее квадратичное его координат:

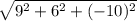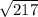
|a|= $\sqrt{9^2+6^2+(-10)^2}$ = $\sqrt{217}$

Формула скалярного произведения векторов a(a1,a2,a3) и b(b1,b2,b3) - ab=a1*b1+a2*b2+a3*c3

Итого ab=9*(-2)+6*0+(-10)*1=-28

0,0(0 оценок)

Ответ:

KarinaDelacour

09.02.2023 02:54

1. Очевидно, что если сечения шара плоскостью равны, то он отстоят от центра шара на одинаковом расстоянии. Отсюда мы можем найти расстояние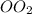 $OO_{2}$ от центра шара до центра круга сечения.

2. Найдем радиус круга в сечении. Из формулы площади круга выражаем радиус.

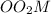3. Рассмотрим прямоугольный треугольник $OO_{2}M$ . В нем угол 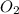$O_{2}$ прямой, поэтому OM (а это радиус шара, который необходим для того, чтобы найти площадь его поверхности) - это гипотенуза. Из теоремы Пифагора находим радиус шара.

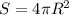4. Площадь поверхности шара: $S=4\pi R^{2}$ . Подставляем найденный чуть выше радиус вместо R и получаем ответ.

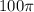
ответ: $100\pi$