1)Sabc=1/2*2*2√3=2√3(по формуле S прямоугольного треугольника)
2)Тут два варианта(находим сторону AC)
Первый : треуг. ABC-прямоугольный:
по т. Пифагора: АС^2=(2√3)^2+4=16. АС=4
Второй : угол ВАС=30° в прямоугол треуг АВС. Отсюда по св-ву
АС=2ВС=4
3)треуг ДАС: по т о сумме углов треугольника: угол СДА+угол ДСА+угол САД=180°. Отсюда угол САД=45°=угол СДА-по призн треуг СДА-р/б треугольник-по опр АС=СД =4
4)Sсda=4*4*1/2=8(по формуле S прямоугольного треугольника)
5)Sabcd=Sсda+Sabc=8+2√3
ответ: 8+2√3
2√3+8
Объяснение:
1) ΔАВС.
а=ВС=2, h=АВ=2√3
2) ΔАВС (∠В=90°).
Напротив угла в 30° лежит катет, равный половине гипотенузы:
АС = 2 * ВС = 2*2=4
3) ΔACD (∠C=90°) : ∠А = 90°-∠D = 90°-45°=45° ⇒ ΔACD - равнобедренный ⇒ DC=AC=4
4)
5) S (ABCD) = S(ABC)+S(ACD)=2√3+8
1)Sabc=1/2*2*2√3=2√3(по формуле S прямоугольного треугольника)
2)Тут два варианта(находим сторону AC)
Первый : треуг. ABC-прямоугольный:
по т. Пифагора: АС^2=(2√3)^2+4=16. АС=4
Второй : угол ВАС=30° в прямоугол треуг АВС. Отсюда по св-ву
АС=2ВС=4
3)треуг ДАС: по т о сумме углов треугольника: угол СДА+угол ДСА+угол САД=180°. Отсюда угол САД=45°=угол СДА-по призн треуг СДА-р/б треугольник-по опр АС=СД =4
4)Sсda=4*4*1/2=8(по формуле S прямоугольного треугольника)
5)Sabcd=Sсda+Sabc=8+2√3
ответ: 8+2√3
2√3+8
Объяснение:
1) ΔАВС.
Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h).а=ВС=2, h=АВ=2√3
2) ΔАВС (∠В=90°).
Напротив угла в 30° лежит катет, равный половине гипотенузы:
АС = 2 * ВС = 2*2=4
3) ΔACD (∠C=90°) : ∠А = 90°-∠D = 90°-45°=45° ⇒ ΔACD - равнобедренный ⇒ DC=AC=4
4)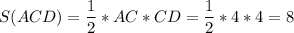
5) S (ABCD) = S(ABC)+S(ACD)=2√3+8