1) Точка, лежащая на единичной окружности имеет абсциссу, равную косинусу соответствующего угла, а ординату , равную синусу этого угла.
То есть, если точка А лежит на единичной окружности, то её координаты можно записать так: .
Основное тригонометрическое тождество имеет вид: .
Поэтому проверяем это тождество для заданных координат.
На единичной окружности лежит точка .
Найдём значение угла, соответствующего точке В, лежащей на единичной окружности.
Смотри рисунок.
Так как sin любого угла не превосходит 1, то полученный результат говорит о том, что треугольника с такими размерами не существует. Решения задача не имеет .
N 8:
Для начала найдем площадь более темно закрашенной фигуры:
воспользуемся формулой площади треугольника S =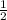 × a × b × sin ∠(a,b)
× a × b × sin ∠(a,b)
S =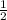 × 12 × 12 × sin 120° = 36√3 см²
× 12 × 12 × sin 120° = 36√3 см²
Теперь площадь менее темно закрашенной фигуры:
воспользуемся формулой площади сектора S = π × R² ×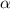 / 360°, а потом отнимем от полученной площади площадь более темно закрашенной фигуры:
/ 360°, а потом отнимем от полученной площади площадь более темно закрашенной фигуры:
S = π × 12² × 120° / 360° - 36√3 = 48π - 36√3 см² (не был уверен что нужно подставлять значение числа π, ведь об этом ничего не сказано)
N 9:
Для начала найдем диаметр по формуле длинны отрезка по координатам: √((х₁ - х₂)² + (y₁ - y₂)²)
d = √136 = 2√34, тогда R = √34
Далее по формуле площади круга решаем: S = π × R² = 34π
1) Точка, лежащая на единичной окружности имеет абсциссу, равную косинусу соответствующего угла, а ординату , равную синусу этого угла.
То есть, если точка А лежит на единичной окружности, то её координаты можно записать так: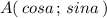 .
.
Основное тригонометрическое тождество имеет вид: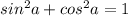 .
.
Поэтому проверяем это тождество для заданных координат.
На единичной окружности лежит точка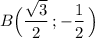 .
.
Найдём значение угла, соответствующего точке В, лежащей на единичной окружности.
Смотри рисунок.
Так как sin любого угла не превосходит 1, то полученный результат говорит о том, что треугольника с такими размерами не существует. Решения задача не имеет .