Геометрия: решить две задачи по геометрии

решить две задачи по геометрии

Показать ответ

Ответ:

анора10

28.03.2022 06:13

а) BC1 || AD1, поэтому угол между прямыми AB1 и BC1 равен углу между AB1 и AD1.

ребро куба равно а, поэтому (так как грани куба - квадраты), то AB1=AD1=B1D1, а значит треугольник AB1D1 - правильный(равносторонний),

углы равностороннего треугольника равны 60 градусов,

значит искомый угол между прямыми AB1 и BC1 равен 60 градусов

б) так как В1С1 - перпендикуляр с точки С1 на грань АА1В1В, то угол между прямой AC1 и гранью AA1B1B равен углу В1АС1

(треугольник АВ1С1 - прямоугольным с прямым углом АВ1С1)

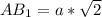
по свойству диагонали квадрата $AB_1=a*\sqrt{2}$

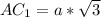
по свойству диагонали куба $AC_1=a*\sqrt{3}$

$cos (B_1AC_1)=\frac{AB_1}{AC_1}=\frac{a\sqrt{2}}{a\sqrt{3}}=\sqrt{\frac{2}{3}}$

угол В1АС1 равен arccos корень(2/3)т.е.

угол между прямой AC1 и гранью AA1B1B равен arccos корень(2/3) градусов

Надо! длина ребра куба abcda1b1c1d1 равна а. вычислить угол между а) прямыми ab1 и bc1 ; б) прямой a

0,0(0 оценок)

Ответ:

vadar22222

15.06.2020 04:16

1.
$x_a= \frac{1}{3}x_m-x_n= \frac{1}{3}\cdot (-3)-2=-1-2=-3 \\ \\ y_a= \frac{1}{3}y_m-y_n= \frac{1}{3}\cdot (6)-(-2)=2+2=4$

ответ. $\vec{a}(-3;4)$

2.
уравнение окружности с центром в точке А и радиусом R имеет вид:

(x+3)²+(y-2)²=R²
Чтобы найти R подставим координаты точки В в это уравнение
(0+3)²+(-2-2)²=R²
9+16=R² R²=25
ответ. (x+3)²+(y-2)²=25

3.
$MN= \sqrt{(x_N-x_M)^2+(y_N-y_M)^2} = \sqrt{(2-(-6))^2+(4-1)^2} =\\ \\= \sqrt{73}$
$MK= \sqrt{(x_K-x_M)^2+(y_K-y_M)^2} = \sqrt{(2-(-6))^2+(-2-1)^2}= \\ \\ = \sqrt{73}$
Высота равнобедренного треугольника,проведенная к основанию, является и медианой.
Середина отрезка КN точка С имеет координаты
$x_C= \frac{x_K+x_N}{2}= \frac{2+2}{2}=2 \\ \\ y_C= \frac{y_K+y_N}{2}= \frac{4+(-2)}{2}=1$

$MK= \sqrt{(x_C-x_M)^2+(y_C-y_M)^2} = \sqrt{(2-(-6))^2+(1-1)^2}=8$

4.
Пусть координаты точки N, лежащей на оси ох:
N (a;0)
Так как по условию точка N равноудалена от точек Р и К, то NP=NK
или

$\sqrt{(x_P-x_N)^2+(y_P-y_N)^2 }=\sqrt{(x_K-x_N)^2+(y_K-y_N)^2 } \\ \\ \sqrt{(-1-a)^2+(3-0)^2 }=\sqrt{(0-a)^2+(2-0)^2 } \\ \\$

Возводим в квадрат
1+2а+а²+9=a²+4
2a=-6
a=-3

ответ. N(-3;0)

0,0(0 оценок)

Популярные вопросы: Геометрия