Решить треугольники, молю, завтра сдавать

(ед.)

Объяснение:

Дано: ΔАВС - прямоугольный.

АС = 3; АВ = 4; ВС = 5.

Окр. O,r - вписанная.

ЕК ⊥ ВС.

Найти: ЕК.

1. Рассмотрим АМОР.

∠А = 90° (условие);

Радиус, проведенный в точку касания перпендикулярен касательной.

⇒ ОР ⊥ АС; ОМ ⊥ АВ.

Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ АМ || АР; АР || МО.

⇒ АМОР - прямоугольник.

Противоположные стороны прямоугольника равны.

⇒ АМ = АР; АР = МО.

МО = АР = r ⇒ АМ = АР = АР = МО.

⇒ АМОР  - квадрат.

2. Найдем r по формуле:

, где a и b - катеты, с - гипотенуза.

⇒ АМ = АР = АР = МО=1

3. Рассмотрим ΔАВС и ΔМВН - прямоугольные.

∠В - общий;

⇒ ΔАВС ~ ΔМВН (по двум углам).

Составим отношение сходственных сторон:

4. Рассмотрим ΔЕМО и ΔОКН - прямоугольные.

МО = ОК = r

∠1 = ∠2 (вертикальные)

⇒ ΔЕМО = ΔОКН (по катету и острому углу)

⇒ ЕО = ОН (как соответственные элементы)

МО +ОН = ЕО + ОК = МН =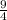

⇒

Объяснение:

1) Перша ознака подібності трикутників (за двома кутами)

    Якщо два кути одного трикутника відповідно дорівнюють двом кутам другого трикутника, то такі трикутники є подібними.

2) Друга ознака подібності трикутників (за двома сторонами і кутом між ними)

    Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то такі трикутники є подібними.

3) Третя ознака подібності трикутників (за трьома сторонами)

    Якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники є подібними.